6.2     Апроксимація даних

 

     Апроксимація (Approximation) взагалі – це наближений опис однією функцією (апроксимувальною) заданого вигляду іншої функції (апроксимованої), яка задається у будь-якому вигляді (при апроксимації даних вона задається у вигляді масивів даних).

     Існує два головних підходи до апроксимації даних. При одному з них вимагають, щоб апроксимувальна крива (можливо кусково-гладка) проходила через всі точки, які задані таблицею. Це можна зробити з допомогою методів інтерполяції, які були розглянуті в попередньому розділі. При іншому підході дані апроксимують простою функцією, яка використовується при всіх табличних значеннях, але не обов’язково, щоб вона проходила через всі точки. Такий підхід зветься припасуванням кривої, яку прагнуть провести так, щоб її відхилення від табличних даних був мінімальним. Як правило, користуються методом найменших квадратів (МНК), тобто зводять до мінімуму суму квадратів різниць між значенням функції, яка визначена обраною кривою, та таблицею.

     Нехай у таблиці задана точка і треба знайти апроксимувальну криву в діапазоні (рис. 6.11). В цьому випадку похибка в кожній табличній точці буде

     Тоді сума квадратів похибок визначається виразом:

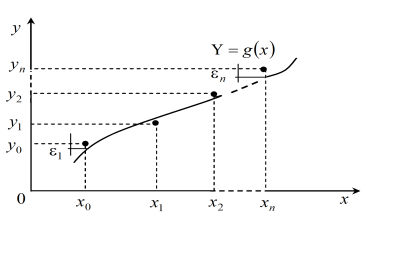
Рисунок 6.11 – Апроксимація даних

 

Як правило, функцію обирають у вигляді лінійної комбінації вибраних функцій

     Умова мінімуму Е визначається рівнянням:

     Відомо, що

ця умова еквівалентна системі рівнянь:

 

     (6.20)

* = .

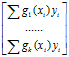     Елементи матриці в лівій частині та вектора-стовпця в правій визначаються табличними даними, тому отримана система k лінійних рівнянь з k невідомими може бути розв’язана.

Якщо перейти до матричної форми запису, то формула методу найменших квадратів матиме вигляд:

,

де , , .

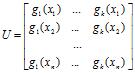Вибір виду функції повинен здійснюватися з урахуванням характеру табличних даних (періодичності, властивості симетрії, існування асимптотики та т. п.).

     Іноді таблицю розбивають на декілька частин та добирають окрему апроксимувальну криву для кожної частини. Такий підхід задовольняє ті випадки, коли дані відповідають різним фізичним станам системи.

     Залишкова середня квадратична похибка апроксимації оцінюється:

     Якщо при побудові апроксимувальної функції використовуються ортогональні поліноми, для яких

, якщо

то система (6.5) спрощується, і матриця стає діагональною. Коефіцієнти визначаються зі співвідношень

     Це спрощує задачу, і тому в багатьох стандартних програмах припасування кривих використовують ортогональні поліноми.

     Метод найменших квадратів може бути застосований, якщо функція матиме нелінійний характер. При цьому потрібно використовувати заміни, що дозволять лінеарізувати функцію і знайти коефіцієнти за допомогою МНК. У таблиці 6.2 наведені типові лінеаризуючі заміни.

Таблиця 6.2

Лінеаризуючі заміни до функції

Апроксимуюча функція	Необхідна заміна