6.1.3.2 Створення сплайнових параметричних кривих

 

Особливість сплайнових параметричних кривих полягає в вираженні невідомих коефіцієнтів сплайна через похідні в визначених точках кривої. Такий прийом зменшує кількості невідомих полінома. Також потрібно відмітити простоту переходу запису параметричних кривих від одного до багатьох вимірів.

Криві і поверхні можуть бути представлені явно, неявно і параметрично. Параметричне представлення дуже широко застосовується в комп'ютерній графіці через простоту та універсальність представлення. В наступних підрозділах наведено приклади знаходження невідомих коефіцієнтів та безпосередньо самих параметричних кривих.

Нехай необхідно побудувати кубічну параметричну криву, визначену трьома точками та тангенсом нахилу кривої в середній точці (рис.6.4).

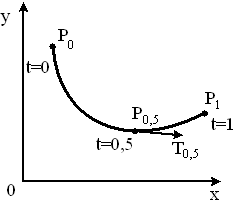
Рисунок 6.4 – Типова крива при побудові сплайна за трьома точками і значенням похідної в середній точці

 

Спершу побудуємо криву для змінної (рис. 6.5). На криву накладається чотири обмеження для знаходження всіх чотирьох параметрів.

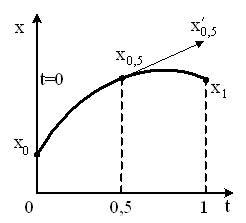
Рисунок 6.5 – Побудова кривої для змінної

 

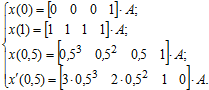               (6.11)

Запишемо рівняння (6.11) в матричному вигляді.

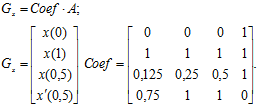               (6.12)

     З рівняння (6.12) досить просто знаходимо матрицю невідомих коефіцієнтів :

                         (6.13)

     Підставивши (6.12) у вираз (6.13), отримаємо:

                    (6.14)

     Матрицю зазвичай називають базисною. Для зручності запису виконаємо заміну . В нашому випадку матриця рівна:

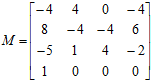
     Помноживши матрицю та матрицю , отримаємо сім’ю базових функцій . Вони виконують роль основних складових компонентів для створення геометричних утворень з різними ваговими коефіцієнтами. Тобто,

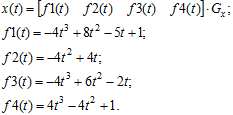          (6.15)

     Зобразимо функції (6.15) на рис. 6.6.

Невідомі коефіцієнти для змінних та знаходяться аналогічно. Базова матриця та базові функції залишаються незмінними, змінюється лише геометричний вектор . Тому загальне параметричне рівняння матиме вигляд:

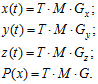
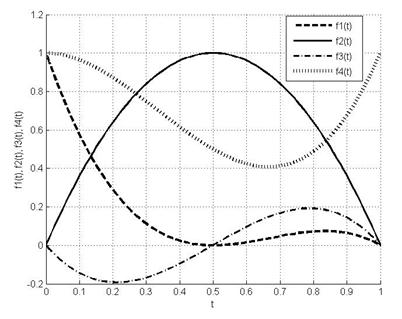
Рисунок 6.6 – Базові функції

 

В цьому прикладі розглядається побудова ермітової кривої (Hermitian curve) (рис. 6.7), яка задається координатами двох крайових точок та значеннями їх похідних (дотичних).

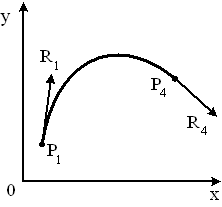
Рисунок 6.7 – Приклад побудови ермітової кривої

    

Визначимо рівняння для побудови ермітової кривої через геометричний вектор: . Виконаємо дії, аналогічні до попереднього пункту. Запишемо систему рівнянь для розрахунку невідомих коефіцієнтів:

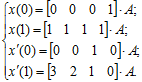                    (6.16)

В матричному вигляді рівняння (6.16) запишеться . Звідки коефіцієнт розраховується як , . В нашому випадку матриця рівна,

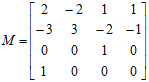
Подібно до попереднього прикладу розрахуємо параметричну криву помноживши матрицю на матрицю . Отримаємо сім’ю базових функцій :

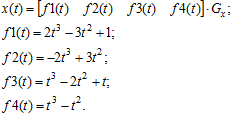               (6.17)

     Зобразимо функції (6.17) на рис. 6.8.

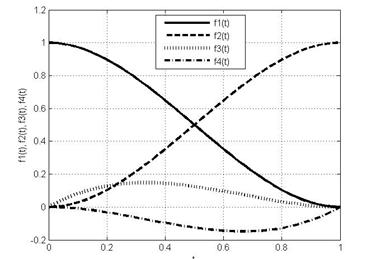
Рисунок 6.8 – Базові ермітові функції

 

Криві Без’є (Bezier Curves) – головний елемент побудови криволінійних форм у всіх без виключення програмах комп’ютерної графіки; за їх допомогою можливо досить точно апроксимувати будь-яку лінію змінної кривизни.

Крива Без’є це один з найпоширеніших видів гладких параметричних кривих. Ці криві знайшли широке застосування в сучасних CAD системах. Також вони стали невід’ємною частиною операційної системи Windows (наприклад, вони використовуються для відображення шрифтів), і тому функція побудови кривих Без’є входить в стандартний набір функцій Windows GDI+. Криві Без’є за своєю суттю є варіацією ермітових кривих. Вони вказані чотирма точками (рис. 6.9).

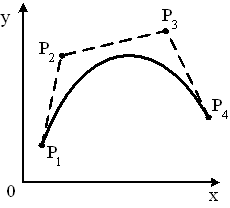
Рисунок 6.9 – Крива Без’є

Визначимо рівняння для побудови ермітової кривої через геометричний вектор

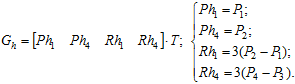          (6.18)

Виконаємо дії, аналогічні до попереднього пункту. Запишемо систему рівнянь для розрахунку невідомих коефіцієнтів:

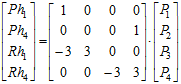
Загальне параметричне рівняння запишеться в вигляді:

де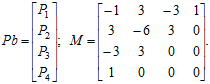

Сім’я базових функцій для кривих Без’є записується:

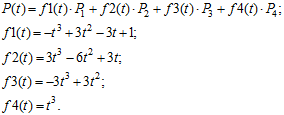     (6.19)

     Зобразимо функції (6.19) на рис. 6.10.

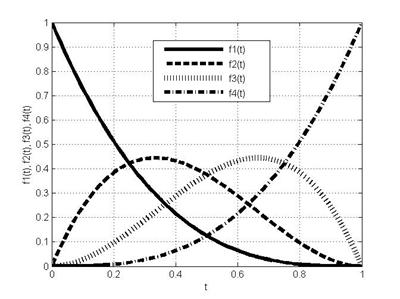
Рисунок 6.10 – Базові функції Без’є

Базові функції Без’є мають властивість опуклості. Крива ніколи не проходитиме через ламану, сформовану чотирма заданими вершинами. Функції Без’є задовольняють умови опуклості, а саме: