6.1.3.1 Класичний кубічний сплайн

 

     Розглянемо найбільш відомий й поширений інтерполяційний сплайн порядку 3 дефекту 1. Ці сплайни порівняно недавно почали широко вживатися в обчислювальній математиці. В машинобудівельному кресленні вони застосовуються багато років, тому що це і є лекала чи гнучкі лінійки, які деформуються так, щоб з їх допомогою можна було провести криву через задані точки Можна показати (вживаючи теорію згину брусу при малих деформаціях), що сплайн – це група сполучених кубічних багаточленів, в місцях сполучення яких перша та друга похідні безперервні. Такі функції звуться кубічними сплайнами. Для їх побудови необхідно задати коефіцієнти, які однозначно визначають поліном у проміжку між двома точками.

Наведемо математичний опис кубічних сплайнів:

Нехай на відрізку дійсної осі задана сітка , в вузлах якої визначені значення функції . Потрібно побудувати на відрізку неперервну функцію – сплайн , яка задовольняє такі вимоги:

1) На кожному відрізку сплайн є багаточленом третього степеня:

(6.5)

2) У вузлах сплайн приймає задані значення , , тобто

                    (6.6)

Умови (6.6) потрібні для проходження сплайнів через вузли заданої сітки , . Попередні дві умови утворюють рівнянь.

3) У внутрішніх вузлах , сплайн має неперервну першу і другу похідну, тобто:

В точках спряження сплайнів, їх перші та другі похідні повинні бути рівними. Таких умов . Для знаходження сплайна потрібно знайти коефіцієнти , , , багаточленів , , тобто невідомих, які задовольняють рівнянь.

Для отримання розв’язку системи потрібно два додаткових рівняння. Їх отримують, визначивши значення кривизни графіка сплайна на кінцях:

Якщо , тоді такий сплайн називають природним. Коли є додаткові відомості про поведінку функції на кінцях інтервалу інтерполяції, то записуються інші краєві умови. Таким чином, кубічний сплайн «склеєний» з кубічних парабол проходить через задані точки, є гладеньким і має безперервну кривизну.

Для побудови кривої (6.5) розраховується чотири коефіцієнти. Запишемо вираз (6.5) у формі, що дозволяє зменшити кількість обчислювальних операцій, запропонованій Чарльзом Ермітом.

Введемо позначення:

                    (6.7)

де – довжина підінтервалу; і – допоміжні змінні; – проміжна точка на відрізку .

Штучною змінною виконується нормалізація змінної на кожному відрізку інтерполювання між двома вузловими точками сітки.

Якщо , то ; якщо , то .

Тобто, коли приймає всі значення в інтервалі , змінна змінюється від 0 до 1, а змінна змінюється від 1 до 0.

     Поліноміальний сплайн третього степеня, що має неперервну першу та другу похідні на відрізку , запишеться:

          (6.8)

Номер сплайна збігається з індексом кінцевої точки відрізка . Для запису виразу сплайна на сусідньому -му відрізку достатньо в (6.8) зменшити всі індекси на одиницю:

          (6.9)

Змінні і визначаються відповідно до конкретного відрізка інтерполяції, тому вирази (6.8) та (6.9) містять фактично різні змінні і . Знайдемо значення сплайна на кінцях відрізка .

Маємо є початком для відрізка , тому , і відповідно до (6.6) .

На кінці відрізка , , отримаємо .

Для інтервалу точка є кінцевою, тому , з формули (6.9) отримаємо .

Отже, виконується умова неперервності функції у вузлах спряження кубічних багаточленів і функція інтерполює задані значення незалежно від вибору похідних . Для зручності запису в подальших розділах зробимо заміну .

Для того, щоб визначити коефіцієнти , , продиференціюємо (6.8) двічі як складну функцію від , враховуючи, що та . Тоді

 

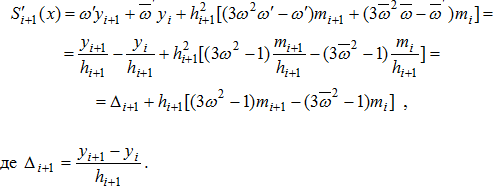
Зменшуючи індекс на одиницю, отримаємо:

               (6.10)

Для сплайна (6.9) виконується умова рівності другої похідної у внутрішніх точках інтерполяційної сітки. Тому для знаходження невідомих коефіцієнтів записують систему рівнянь , використовуючи (6.10). Однозначний розв’язок системи отримаємо введенням додаткових крайових умов.