6.4.4 Формула Гаусса

 

Формула Гаусса називається формулою найвищої алгебраїчної точності. Для формули вигляду (6.24) найвища точність може бути досягнута для поліномів степеня , які визначаються постійними

     Завдання полягає у визначенні коефіцієнтів і абсцис точок .

     Для знаходження цих постійних розглянемо виконання формули (6.24) для функцій вигляду

     Враховуючи, що

,

отримаємо систему рівнянь

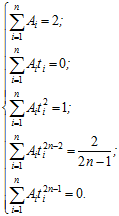          (6.27)

Ця система нелінійна, і її звичайне розв’язання пов’язане із значними обчислювальними труднощами. Але якщо використовувати систему для поліномів вигляду

де – поліном Лежандра, тоді її можна звести до лінійної відносно коефіцієнтів з заданими точками . Оскільки степені поліномів в співвідношенні не перевищують , повинна виконуватися система (6.27) і формула (6.24) приймає вигляд

          (6.28)

В результаті властивості ортогональності ліва частина виразу (6.28) дорівнює 0, тоді

що завжди забезпечується при будь-яких значеннях в точках , які відповідають кореням відповідних поліномів Лежандра.

     Підставляючи ці значення в систему (6.27) і враховуючи перші рівнянь, можна визначити коефіцієнти .

     Формула (6.24), де – нулі полінома Лежандра , а визначаються із системи (6.27), називається формулою Гаусса.

     Значення , для різних наведені в таблиці 6.9.

     Для довільного інтервалу (a,b) формула для методу Гаусса приймає вигляд

де .

     Оцінка похибки формули Гаусса з вузлами визначається із співвідношення

де – максимальне значення 2 похідної на ділянці

     Таблиця 6.9      Елементи формули Гаусса
1 1 0 2
2 1;2 0б57735027 1
3 1;3 0б77459667 =0,55555556
2 0 =0,88888889
4 1;4 0,86113631 0,34785484
2;3 0,33998104 0,65214516

6

1;6

0,93246951

0,17132450

2;5

0,66120939

0,36076158

3;4

0,238619119

0,46791394

7

1;7

0,94910791

0,12948496

2;6

0,74153119

0,27970540

3;5

0,40584515

0,38183006

4

0

0,41795918

8

1;8

0,96028986

0,10122854

2;7

0,79666648

0,22238104

3;6

0,52553142

0,31370664

4;5

0,18343464

0,36268378

6.4.5 Оцінка похибки при чисельному інтегруванні

 

В випадку, коли підінтегральна функція задана аналітично, може бути поставлена задача про знаходження інтеграла с наперед заданою точністю. Оскільки точність розглянутих вище квадратурних формул залежить від кроку h, то точність результату можна підвищити, зменшуючи крок. Наприклад, можна ділити крок пополам. В цьому випадку для оцінки наближення до точного значення інтеграла використовують вже згадуваний метод Рунге:

,

     де – точне значення інтеграла; – наближене значення, отримане з кроком h; – наближене значення, отримане з кроком h/2; р – порядок точності квадратурної формули.

     Тому для знаходження інтеграла з заданою точністю потрібно обрати квадратурну формулу й початковий крок h=h0. Далі розрахувати інтеграл з кроком h/2. Зменшувати крок пополам необхідно до тих пір, поки не виконається умова:

.

Коли ця умова виконана, інтеграл приблизно дорівнює .

 

6.4.6  Алгоритми застосування чисельних методів

 

Послідовність застосування формул Ньютона – Котеса:

1. Вибір формули і знаходження (за допомогою таблиці 6.7) коефіцієнтів .

2. Складання алгоритму та програми, причому:

  •  у випадку завдання дискретних значень через крок ці значення підставляються в (6.21);
  •  у випадку завдання функції значення вираховується, причому

    3. Оцінка похибки.

         Послідовність застосування методу Гаусса:

    1. Вибір порядку методу і знаходження (за допомогою таблиці 6.9) коефіцієнтів і значень

    2. Розбивка інтервалу інтервалів (рисунок 6.15).

    3. Знаходження значень інтервалу для кожного інтервалу

    .

    При цьому значення абсцис всередині кожного інтервалу j знаходяться за формулою

              (6.29)

    де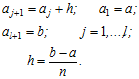

    знаходяться за формулою:

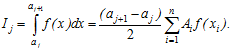              (6.30)

    4. Оцінка похибки .

         В методі Чебишева послідовність дій аналогічна методу Гаусса, але в пункті 1 коефіцієнти беруться з таблиці 6.7, а в пункті 3 для знаходження j-го інтегралу використовується формула

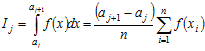         ,      (6.31)

    де оцінюється тим же чином, що і в методі Гаусса, за формулою (6.29)

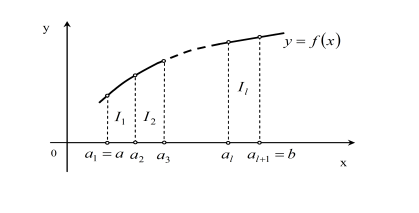
    Рисунок 6.15 – Метод Гаусса. Розбивка інтервалу.