6.4.7 Метод Монте–Карло
Метод чисельного інтегрування Монте–Карло – це найбільш відоме застосування статичного моделювання для розв’язання прикладних математичних задач.
Якщо з послідовністю випадкових чисел 
з законом розподілу ймовірностей 
провести функціональне перетворення
,
то математичне очікування отриманої послідовності випадкових чисел 
(6.32)
при обсязі вибірки більше декількох тисяч чисел з достатньо високою точністю може бути оцінено за формулою
(6.33)
Введемо в вирази (6.29), (6.30) так звану функцію індикатора області
то кінцевий вираз буде мати вигляд
.
Алгоритм обчислення визначеного інтегралу за методом Монте–Карло наведено на рисунку 6.16.
Похибка методу Монте–Карло визначається похибкою генерації псевдовипадкової послідовності чисел, що згенеровані на ЕОМ, та обсягом вибірки. Вона може бути оцінена із співвідношення
(6.34)
де Р – гарантована ймовірність влучання похибки в інтервал 
;
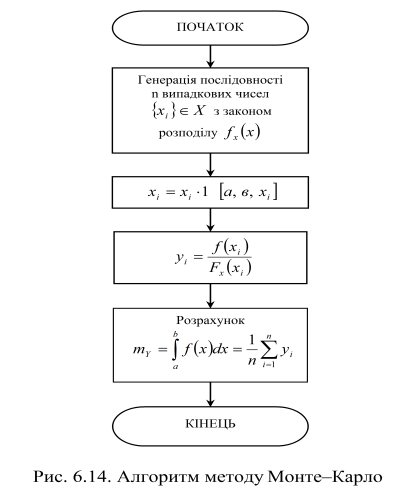
Рисунок 6.16 – Алгоритм методу Монте-Карло
Кількість випробувань n не залежить від кратності інтегралу, тому метод Монте–Карло знаходить застосування для обчислення багатократних інтегралів, де застосовувати інші методи чисельного інтегрування неефективно через сильне збільшення кількості обчислювальних операцій.
Розглянемо послідовність дій при обчисленні кратних інтегралів. Для реалізації цієї процедури перш за все потрібно мати m генераторів випадкових чисел, де m – дорівнює кратності інтегрованих.
Геометрично, обчислення m – кратного інтегралу
(6.35)
де 
– неперервна функція в обмеженій замкненій області S, зводиться до визначення 
– вимірного обсягу прямого циліндра в просторі 
, що побудований на основі S й обмежений зверху поверхнею 
.
Для перетворення інтегралу (6.20) таким чином, щоб нова область інтегрування цілком знаходилась в середині одиничного m – вимірного куба 
, зробимо заміну змінних
де 
– відповідні координати від 0 до 1; 
– граничні значення координат, де розташована область інтегрування.
Тоді з (6.35) отримуємо
де
Якщо застосувати m генераторів рівномірно розподілених випадкових чисел в діапазоні (0,1), то обчислення середнього значення функції від їх комбінацій з застосуванням багатовимірного індикатора області інтегрування дасть шукану оцінку інтегралу
,
де 
дорівнює 1, якщо точка потрапляє в середину області інтегрування, і 0, якщо не потрапляє.
Похибка обчислення m-кратного інтегралу за методом Монте–Карло оцінюється аналогічно однократному за формулою (6.34).
6.5 Чисельне диференціювання
Задача полягає в тому, щоб для заданої диференційованої функції f(x) знайти похідну в точці х0.
6.5.1 Чисельне диференціювання аналітично заданих функцій
Наближене диференціювання аналітично-заданих функцій може бути потрібне при розробці універсальної процедури пошуку похідної для великої кількості різних функцій, або у випадку, коли аналітичний вид похідної надто громіздкий і призводить до втрати точності.
В основі чисельного диференціювання (numerical differentiation) аналітично заданих функцій покладене визначення похідної:
.
Оскільки невідомо, яке значення h узяти, будується послідовність {hk} так, щоб hk®0 (наприклад, 
) і, відповідно, формується послідовність {Dk}, де
, k = 1,2,3,…,n,... (6.36)
Розрахунок елементів послідовності проводять до тих пір, поки виконується умова:
.
Якщо відома точність 
, з якою потрібно знайти похідну, то умова завершення може бути такою:
.
Порядок точності результату в цьому методі – h.
Нехай 
. Тоді порядок точності попереднього метода можна підвищити, використовуючи замість формули (6.36) інші вирази. Розглянемо ці формули.
Формула другого порядку точності O(h2) для обчислення похідної:
.
Отримана формула з наступних міркувань. Розкладемо f(x) в ряд Тейлора:
.
.
Віднімемо з першої рівності другу :
Звідси
Аналогічно можна отримати наступні формули для старших похідних точності порядку O(h2):
,
,
.
Сам алгоритм залишається незмінним. Формується послідовність {hk} так, щоб hk®0 й відповідно обчислюються елементи послідовності {Dk}, для розрахунку яких замість виразу (6.36) використовується одна з отриманих формул.
Існують формули більш високих порядків точності, їх можна знайти в спеціальній літературі.
6.5.2 Чисельне диференціювання таблично заданих функцій
При розв’язанні багатьох практичних задач виникає необхідність визначення похідних від функцій, що задаються масивами даних, отриманих з експерименту. В цьому випадку безпосереднє диференціювання може дати безглузді результати, тому що не відокремлено шум, що дуже сильно впливає на похідну. Приклад зображено на рисунку 6.17, де 
– корисний сигнал,
– сигнал, який виміряний (з шумом).
Зрозуміло, що похідна від 
буде містити дуже сильну випадкову складову, що вносить велику похибку в визначення реальної похідної від х. Практичним шляхом розв’язання цієї проблеми є згладжування сигналу, що отриманий з експерименту, шляхом інтерполяції чи апроксимації, а далі диференціювання інтерполяційного полінома (чи апроксимувальної функції). При цьому для отримання похідних вищих порядків треба ставити умову їх збігання для сигналу та його інтерполяційного полінома. Похибка похідної інтерполяційної функції 
дорівнює похідній від похибки цієї функції:
тобто внаслідок лінійності операцій диференціювання та віднімання маємо
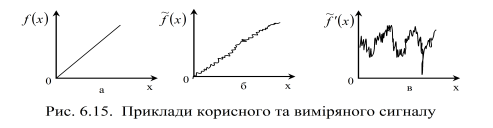
Рисунок 6.17 – Приклади корисного та виміряного сигналу
.
В довідниках існують спеціальні таблиці, що дозволяють знаходити з застосуванням різних різницевих інтерполяційних формул значення похідних. Взагалі такі формули нескладно отримати для будь – яких методів інтерполяції шляхом диференціювання інтерполяційних формул в загальному вигляді.
Контрольні запитання та завдання
1. Сформулюйте задачу інтерполяції. В яких випадках інтерполяція неможлива?
2. З якою точністю можливо обчислити 
за допомогою формули Лагранжа для функції
, якщо вибрати вузли інтерполяції 
?
3. Виведіть інтерполяційну формулу Ньютона для рівновіддалених вузлів.
4. Складіть алгоритм обчислення полінома Лагранжа.
5. Що таке сплайн – інтерполяція? Як визначаються коефіцієнти сплайнів?
6. Опишіть області застосування різницевих методів інтерполяції.
7. Що таке екстраполяція?
8. Якими шляхами розв’язується задача апроксимації?
9. В чому полягає метод Рунге?
10. Чим відрізняється апроксимація від інтерполяції?
11. Виведіть систему рівнянь для визначення коефіцієнтів апроксимувального полінома в методі найменших квадратів.
12. Наведіть формулу метода найменших квадратів.
13. Які поліноми називаються ортогональними? Наведіть приклади.
14. Що таке сплайн?
15. Розробіть алгоритм та наведіть приклад програми для ЕОМ оцінки статистичних характеристик результатів вимірювання випадкової величини Х.
16. Перелічіть методи чисельного інтегрування?
17. Чому необхідні методи і алгоритми чисельного інтегрування?
18. Яка послідовність застосування методів Ньютона – Котеса? Розробіть алгоритм. Чим відрізняються прості формули Ньютона – Котеса від складених?
19. Як отримують формули Ньютона - Котеса? Виведіть прості формули трапецій та Сімпсона для чисельного інтегрування та складені формули.
20. Як застосовуються методи Гаусса і Чебишева? Розробіть алгоритм.
21. Як визначаються коефіцієнти в формулі Гаусса для чисельного інтегрування? Чому її називають формулою найвищої алгебраїчної точності?
22. Як оцінюється похибка методів чисельного інтегрування?
23. Порівняйте методи Чебишева, Гаусса, Ньютона – Котеса?
24. Згадайте метод прямокутників. В чому його суть? Розробіть алгоритм.
25. Розробіть алгоритм та наведіть приклад програми чисельного інтегрування за методом Монте – Карло для двократного інтеграла 
де область інтегрування визначається такими нерівностями
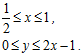
Чи потраплять в область інтегрування точки з координатами (0.55; 0.75), (0.25; 0.75), (0.25; 0.25), (0.99; 0.70)?
26. Коли потрібні методи чисельного диференціювання аналітично заданих функцій і в чому вони полягають?
