Розділ 8. Методи обробки зображень

 

Методи обробки зображень (image processing) мають надзвичайно важливе значення в сучасній науці, вони є одними з таких які безперервно розвиваються та вдосконалюються. При цьому під обробкою зображень розуміють не лише поліпшення зорового сприйняття зображень, але й класифікацію об'єктів, що виконується при аналізі зображень.

Області застосування методів цифрової обробки в наш час значно розширюються, витісняючи аналогові методи обробки сигналів зображень. Методи цифрової обробки широко застосовуються в промисловості, мистецтві, медицині, космосі. Вони застосовуються при керуванні процесами, автоматизації виявлення об'єктів, розпізнаванні образів і в багатьох інших. Цифрова передача зображень із космічних апаратів, цифрові канали передачі сигналів зображень вимагають забезпечення передачі все більших потоків інформації. Формування зображень, поліпшення якості та автоматизація обробки медичних зображень, включаючи зображення, що створюються електронними мікроскопами, рентгенівськими апаратами, томографами тощо, є предметом сучасних досліджень та розробок. Автоматичний аналіз у системах дистанційного спостереження широко застосовується при аналізі місцевості, у лісовому господарстві, наприклад, для автоматичного підрахунку площі вирубок, у сільському господарстві для спостереження за дозріванням урожаю, у розвідці, у системах протипожежної безпеки. Контроль якості виробленої продукції виконується завдяки автоматичним методам аналізу сцен.

Сьогодні важко представити область діяльності, у якій можна обійтися без комп'ютерної обробки зображень. При комп'ютерній обробці зображень вирішується широке коло завдань, таких як поліпшення якості зображень; вимірювання параметрів зображення; спектральний аналіз багатомірних сигналів; розпізнавання зображень; стиск зображень.

 

8.1 Класичні методи обробки зображень

8.1.1 Математичні моделі зображень

Комп'ютерна обробка зображень можлива після перетворення сигналу зображення з безперервної форми в цифрову форму. Ефективність обробки залежить від адекватності моделі, що описує зображення, необхідної для розробки алгоритмів обробки. Модель зображення представляє систему функцій, що описують істотні характеристики зображення: функцію яскравості, що відбиває зміну яскравості в площині зображення, просторові спектри й спектральні інтенсивності зображень, функції автокореляції. Канал

зображення містить оптичну систему, оптико – електричний перетворювач, пристрій аналого-цифрового перетворення (АЦП) і цифрової обробки сигналів зображення.

При обробці зображень широко використовується аналіз спектрів зображень. Спектр зображення (image spectrum) одержують прямим двовимірним перетворенням Фур'є функції, що описує зображення:

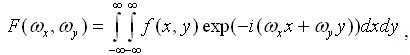, (2.1)

де – просторові частоти; – уявна одиниця.

Функція при фіксованих значеннях просторових частот описує плоску хвилю в площині зображення (x, y) (відповідно до рисунка 1.1).

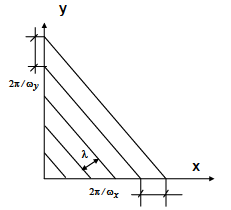
Рисунок 2.1 – Визначення просторових частот зображення

Формула (2.1) пов’язує дійсну функцію, що описує яскравість зображення f(x, y) з комплексною функцією частоти – спектром зображення :

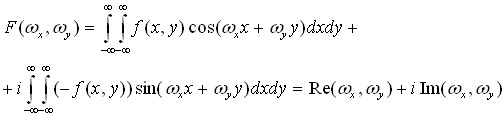(2.2)

де – дійсна частина спектра; – реальна частина спектра.

Амплітуда і фаза спектра визначаються за формулами (2.3) і (2.4) відповідно:

 

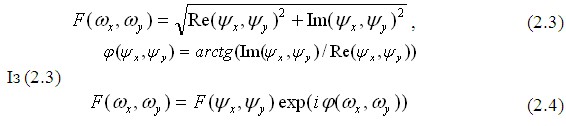
Обернене перетворення Фур’є дозволяє відновити зображення по його спектру:

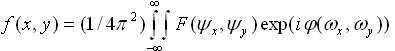(2.5)

Спектральна інтенсивність (spectral intensity) зображення характеризує розподіл енергії по просторових частотах. Вона визначається як квадрат модуля спектра зображення:

(2.6)

Для її назви використовуються терміни спектральна щільність (spectral density) і енергетичний спектр (energy spectrum).

Енергія зображення визначається як інтеграл енергетичного спектра по просторових частотах. Відповідно до теореми Парсеваля енергія зображення може бути обчислена відповідно до 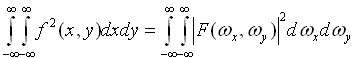(2.7):

(2.7)

Імовірнісні моделі зображень (probabilistic image models) широко використовуються для опису зображень. Зображення в цьому випадку розглядається як випадкова функція просторових координат (x,y) і часу t. Випадковий процес називається стаціонарним у широкому змісті, якщо він має постійні значення математичного очікування й дисперсії, а його автокореляційна функція залежить не від координат, а від їх різниці (зсуву). Випадковий процес називається стаціонарним у вузькому змісті, якщо його n- мірна щільність розподілу ймовірностей інваріантна до зсуву. Випадковий процес описується щільністю розподілу ймовірності яскравості в зображенні по просторових координатах для деякого фіксованого моменту часу t .

У відповідності з визначенням математичне сподівання (середнє значення, mathematical expectation) стаціонарного процесу в широкому змісті

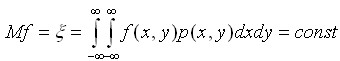(2.8)

Дисперсія (dispersion, variance)

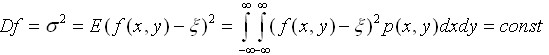(2.9)

Функція автокореляції (autocorrelation function) обчислюється наступним чином:

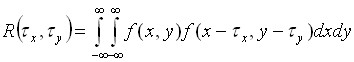(2.10)

де задають зсуви зображення по відповідним осям координат.