8.2.1 Розмірність. Види розмірності
Ключовою величиною що описує фрактал кількісно є "фрактальна розмірність", однак, у різних джерелах під цим терміном розуміють різні величини: розмірність Мінковського, розмірність Хаусдорфа-Безиковича, розмірність самоподібності. Ці величини відрізняються алгоритмом обчислення, але для математичних фракталів є еквівалентними.
Евклідова або вкладена розмірність De (embedding dimension) – об'єкти це набори крапок, поміщені в простір. Іншими словами De – розмірність простору, що включає об'єкт.
Топологічна розмірність Dt – це ціла величина, що характеризує топологічний об'єкт: для лінії Dt = 1для площини – 2, для поверхні – 3. Dt володіє гомеоморфізмом, тобто є інваріантом відносно лінійних перетворень.
Розмірність Хаусдорфа-Безиковича DH – це міра розбивки об'єкта Е на частини розміром r з наступним підрахунком числа N(r) частин, що покривають досліджуваний об'єкт.
Розмірність DH інваріантна щодо лінійних перетворень і для її кількісної оцінки використовується величина, яка називається метричним порядком:
(2.33)
k(E) пов’язана з розмірністю Хаусдорфа-Безиковича співвідношенням:
. (2.34)
Розмірність самоподібності Ds – характеризує регулярні фрактали (крива Кох, трикутник Серпинского й т.д.) і є для них оцінкою розмірності Хаусдорфа-Безиковича. Значення Ds обчислюється точно, тому що можна чітко виділити компоненти подібності й визначити їх масштабний коефіцієнт. Для обчислення Ds використовується співвідношення:
, (2.35)
де N – число компонентів подібності, r – масштабний коефіцієнт.
Таким чином, розмірність самоподібності характеризується співвідношенням:
. (2.36)
Фракталом в широкому сенсі називається множина, у якої розмірність Хаусдорфа-Безиковича DН не співпадає з його топологічною розмірністю DТ .
8.3. Вейвлет-перетворення
Вейвлет-перетворення (wavelet transformation) – це сучасний і перспективний метод обробки даних. Англійське слово wavelet (від французького "ondelette") дослівно перекладається як "коротка (маленька) хвиля". Апарат вейвлет-аналізу одержав свій розвиток на початку 1980-x років у роботах Морле, Гроссмана й деяких інших авторів . Результаты, отримані у різних областях за допомогою вейвлет-аналізу, підсилили інтерес до цього напрямку та сприяють його безупинному розвитку.
Методи вейвлет-аналізу можливо застосувати до даних різної природи. Це можуть бути, наприклад, одномірні функції або двовимірні зображення. Грубу класифікацію вейвлет-алгоритмів можна зробити, виділивши безперервне (CWT – Contіnuous Wavelet Transform) і дискретне (DWT – вDіscrete Wavelet Transform) вейвлет-перетворення. Одержати набір вейвлет-коефіцієнтів у випадку дискретного перетворення швидше, і воно дає досить точне представлення сигналу при меншому обсязі одержуваних у результаті даних. Безперервне перетворення вимагає більших обчислювальних витрат, але, разом із цим, дозволяє детальніше роздивитися структуру сигналу.
На відміну від звичайних спектральних перетворень, вейвлет-аналіз дозволяє з однаковою точністю апроксимувати як гладкі функції, так і функції з різкими випадами, що дає можливість визначати незначні об’єкти. Застосування вейвлетів розглянуто в багатьох роботах, наприклад. Оскільки вейвлет-перетворення представляє собою згортку сигналу зображення з вейвлет-функцією, що зміщується відносно координат, даний метод близький за змістом до методів на основі фільтрації.
Вибір того або іншого методу залежить від поставленого завдання й типу наявних даних, які необхідно обробити, від можливостей обчислювальної техніки і від того, у якому вигляді необхідно представити результат.
Термін вейвлет-перетворення об’єднує два види перетворень – пряме і обернене, які, відповідно, переводять досліджувану функцію 
в набір вейвлет-коефіцієнтів
і назад. Розділяють безперервне та дискретне перетворення
Пряме вейвлет-перетворення здійснюється відповідно до правила
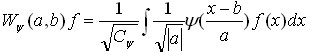(2.37)
де a і b – параметри, що визначають відповідно масштаб і зсув функції 
, яка називається аналізуючим вейвлетом, 
- нормувальний множник. Інтегрування ведуть по всій числовій осі.
Базисний, або материнський вейвлет (parent wavelet) створює за допомогою розтягнень та зсувів сімейство 
.
Маючи відомий набір коефіцієнтів , можна відновити первинний вигляд функції :
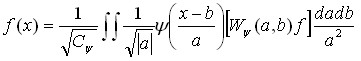(2.38)
Пряме (2.37) і обернене (2.38) перетворення залежать від деякої функції 
, яку називають базисним вейвлетом. Практично єдиним обмеженням на його вибір є умова конечності нормувального множника
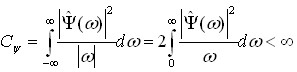(2.39)
де 
– Фур'є- образ вейвлета
: 
.
Безліч функцій задовольняють дану умову, тому можливо підібрати вид вейвлета, який найбільш підходить для рішення конкретного завдання.
Умова (2.37) означає, що Фур'є-образ вейвлета дорівнює нулю при нульовій частоті, тобто 
. Якщо це не так, то знаменник в інтегралі (2.37) збігається до нуля, у той час як чисельник має відмінне від нуля значення, і коефіцієнт перестає бути кінцевим.
У свою чергу, цю вимогу можна представити в іншому виді. Оскільки Фур'є-образ при нульовій частоті має вигляд
, ми можемо вимагати рівність нулю інтеграла від вейвлета по всій осі:
(2.40)
Головні ознаки вейвлета
В якості базисних функцій, що утворюють ортогональний базис, можна використовувати широкий набір вейвлетів. Для практичного застосування важливо знати ознаки, якими неодмінно повинна володіти вихідна функція, щоб стати вейвлетом. Приведемо основні з них.
Обмеженість. Квадрат норми функції повинен бути конечним:
(2.41)
Локалізація. ВП на відміну від перетворення Фур'є використовує локалізовану вихідну функцію і у часі, і по частоті. Для цього досить, щоб виконувалися умови:
і 
, при 
(2.42)
Нульове середнє. Графік вихідної функції повинен бути знакозмінним навколо нуля на осі часу і мати нульову площу
(2.43)
Рівність нулю площі функції 
, тобто нульового моменту, призводить до того, що Фур'є - перетворення 
цієї функції дорівнює нулю при 
і має вигляд смугового фільтра.
Автомодальність. Характерною ознакою ВП є його самоподібність. Всі вейвлети конкретного сімейства 
мають те ж число осциляцій, що й материнський вейвлет , оскільки отримані з нього за допомогою масштабних перетворень (a) і зсува (b).
Приклади материнських вейвлетів
Основні функції, які створюють вейвлети, так звані материнські вейвлети, наведені в табл. 2.1.
Таблиця 2.1
Материнські вейвлети
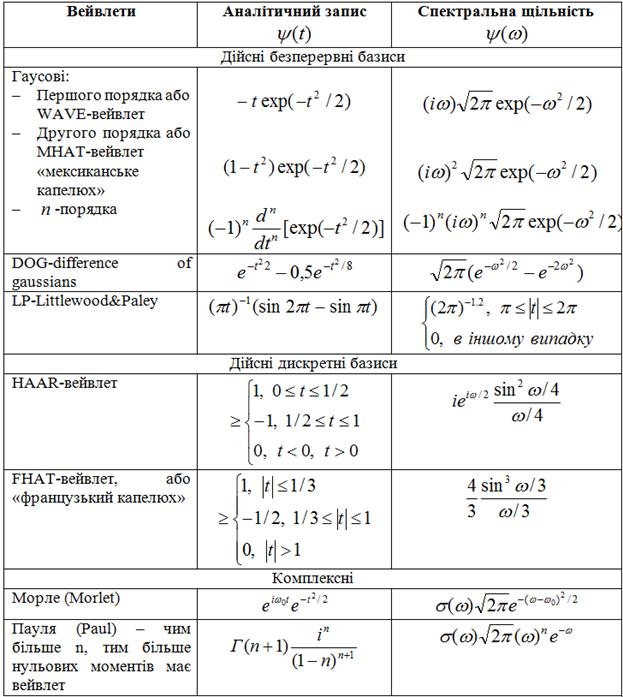
Найбільш поширені базиси створюються на основі похідних функції Гауса 
. Це обумовлено тим, що функція Гауса має найкращі показники локалізації як у часовій, так і в частотній областях.
На рис. 2.15 показані вейвлети перших чотирьох порядків і модулі їх спектральної щільності. При n =1 одержуємо вейвлет першого порядку, який називається WAVE - вейвлетом з нульовим моментом рівним нулю. При n = 2 одержуємо MHAT – вейвлет, що називається "мексиканський капелюх" (mexіcan hat – схожий на сомбреро). У нього нульовий і перший моменти дорівнюють нулю.
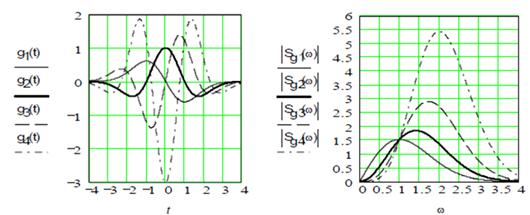
Рисунок 2.15 – Вейвлети перших чотирьох порядків
Найбільш простий приклад дискретного вейвлета – це HAAR-вейвлет. Його недоліком є несиметричність форми та не гладкість – різкі границі в t-області. Серед комплексних вейвлетів найбільше часто використовується базис, заснований на добре локалізованому у часовій та в частотної областях вейвлеті Морле. Характерний параметр 
дозволяє змінювати вибірковість базису. Дійсна та уявна частини – це амплітудно-модульовані коливання.
Вище був представлений невеликий перелік типів вейвлетів, що аналітично описуються в явному вигляді. Однак більшість типів вейвлетів не мають аналітичного опису у вигляді однієї формули, а задаються ітераційними виразами, які легко обчислюються комп’ютерами. Прикладом таких вейвлетів є функції Добеши (Daubechіes), одна з яких (db4) використовується в якості вбудованої в Mathcad.
У наш час вибір вейвлетов досить великий. Тільки в пакеті Wavelet Toolbox (MATLAB ) представлено півтора десятка материнських вейвлетів; при цьому для ряду з них дано ще безліч варіантів. Для одержання довідки про будь-який тип вейвлета при роботі в командному режимі MATLAB досить виконати команду waveіnfo ('type'), указавши тип вейвлета. Для перегляду вейвлетів достаточно виконати команду wavemenu і у вікні, що з'явилося, зі списком розділів вейвлет перетворень нажати кнопку Wavelet Dіsplay. Натискання цієї кнопки виводить вікно перегляду вейвлетів, у якому можна переглядати: обраний вейвлет (з ім'ям 'Name') та інформацію про нього.
Вибір конкретного материнського вейвлета цілком залежить від характеру поставленого завдання та від конкретного аналізованого сигналу.
При обробці зображень доводиться мати справу з двовимірними масивами S(x, y) . Вони задаються в просторі 
, як функції двох змінних x і y . У цьому випадку двовимірна вейвлет-функція має вигляд:
(2.44)
де 
і 
, 
і 
– значення a і b по кожному виміру.
Для вейвлет-перетворень (ВП) дискретних зображень батьківський та материнський вейвлети будують наступним чином:
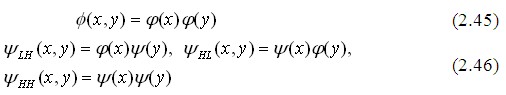
де індекси H і L означають реалізацію фільтрів високих частот та низьких частот складових.
Тоді двовимірні вейвлети запишуться в такому вигляді:
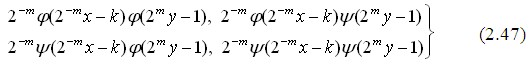
Таким чином, на двовимірній площині відбувається аналіз по горизонталі, вертикалі й діагоналі з однаковим розширенням відповідно до трьох наведених вище вейвлетів.
Формули дискретного ВП двовимірних сигналів і зображень, створені з врахуванням наведених вище співвідношень (2.47), використані в пакеті Wavelet Toolbox.
Пряме ВП зображення відбувається таким способом. Припустимо, що маємо зображення розміром 
(рис. 2.16, а). Спочатку кожний з N рядків зображення ділиться (фільтрується) на низькочастотну (НЧ) і високочастотну (ВЧ) половини. У результаті виходить два зображення розміром 
(рис. 2.16, б). Далі кожний стовпець ділиться так само, у підсумку виходить чотири зображення розміром 
(рис. 2.16, в): НЧ по горизонталі та вертикалі (НЧНЧ1), ВЧ по горизонталі та вертикалі (ВЧВЧ1), НЧ по горизонталі та ВЧ по вертикалі (НЧВЧ1) і ВЧ по горизонталі та НЧ по вертикалі (ВЧНЧ1). Перше із зазначених вище зображень ділиться аналогічним чином на наступному кроці (рівні) перетворення (рис. 2.16, г) і т.д.
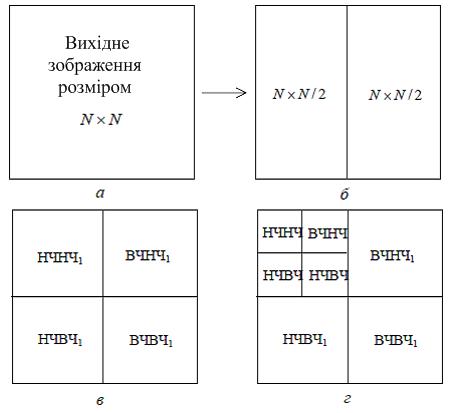
Рисунок 2.16 – Пряме ВП зображення
Для прикладу розглянемо як можна здійснити видалення шумів та компресію зображень за допомогою ВП. Для вирішення даної задачі здійснюється граничне обмеження рівня коефіцієнтів, що деталізують. Задавши певний поріг і "відтинаючи" коефіцієнти нижче цього порога, можна значно знизити рівень шуму і стиснути зображення.
Нижче наведений фрагмент програми фільтрації зображення від шумів, що завантажене з файлу noіse. При цьому використані функції wpbmpen (установка глобального порога) і wpdencmp (видалення шумів і стиск зображень) :
load noissi2d; nbc = size(map,1); wname = 'db8';
lev = 2; tree = wpdec2(X,lev,wname);
det1 = [wpcoef(tree,2) wpcoef(tree,3) wpcoef(tree,4)];
sigma = median(abs(det1(:)))/0.6745; alpha = 1.1;
71
thr = wpbmpen(tree,sigma,alpha); keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);
colormap(pink(nbc));
subplot(221), image(wcodemat(X,nbc));
title('Вихідне зображення')
subplot(222), image(wcodemat(xd,nbc));
title('Відфільтроване зображення')
end
На рисунку 2.17 наведені вихідне і відфільтроване зображення, отримані при виконанні програми.
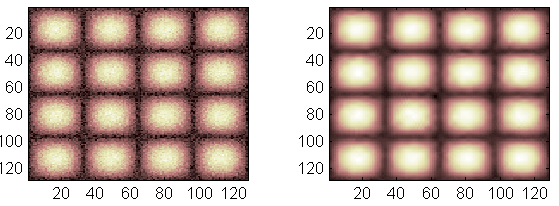
Рисунок 2.17 – Вихідне і відфільтроване зображення
Ряд прикладів по аналізу та реконструкції зображень, їх компресії та фільтрації від шуму даний у розділі GUІ Wavelet Toolbox, що активізується кнопкою Wavelet-2D.
На рис. 2.18 наведено приклад застосування Wavelet-2D: у верхньому лівому куті наведено реальне зображення; у нижньому правому куті дано його вейвлет-розклад (dwt) на прямокутні сегменти; у лівому нижньому куті реконструкція зображення (іdwt); у правому верхньому куті ілюструється ділянка декомпозиції зображення.
До стиску зображень проявляється значний інтерес в усьому світі. Це обумовлено стрімким розвитком цифрової техніки обробки зображень, кольорових принтерів, графічних моніторів, цифрових фото- і відеокамер тощо. Зображення, представлене в цифровому вигляді, має досить великий обсяг у бітах. Наприклад, кольорове зображення розміром 512х512 вимагає для свого зберігання 768 кбайт, а якщо передавати відео послідовність таких зображень зі швидкістю 25 кадрів у секунду, тео необхідна швидкість складе 188 Мбит/с.
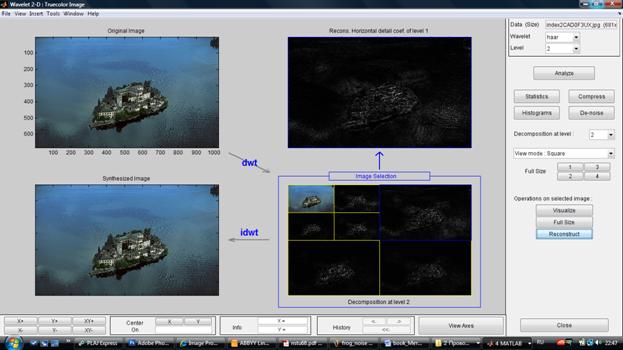
Рисунок 2.18 – Wavelet-2D
Принципова відмінність процедури компресії за допомогою ДВП від широко розповсюдженого стиску за стандартом JPEG полягає в тому, що він працює з усім зображенням, у той час як в JPEG зображення розбивається на блоки, які стискуються незалежно. У випадку ВП можна підібрати таку базисну вейвлет-функцію, що адаптована до найбільш інформативних особливостей зображення. Під адаптивністю мають на увазі, що елементи або ділянки зображення з досить плавною зміною яскравості представляються невеликим числом вейвлет- коефіцієнтів.
Рисунок 2.19 – Стиск зображення з використанням ВП
