Розділ 9 Інтервальний аналіз

 

Основний інструмент, що використовується в інтервальному аналізі (interval analysis), оснований на дуже простій ідеї оточення дійсних чисел інтервалами і векторів областями прямокутної форми – паралелетопами. При цьому вперше з’являється можливість отримати гарантовану оцінку результатів комп’ютерних обчислень прямим переходом до інтервальних змінних в класичних чисельних алгоритмах, що використовуються зазвичай в обчисленнях з плаваючою точкою. Зовсім нещодавно інтервальний аналіз дозволив будувати алгоритми диференціювання, що не мали раніш аналогів, спеціально розроблені для роботи з множинами. Це дало можливість використовувати чисельні методи для доведення тверджень стосовно множин. Таким чином, алгоритми, що базуються на інтервальному аналізі, доповнюють алгоритми на основі комп’ютерної алгебри. Алгоритми на основі інтервального аналізу володіють тією перевагою, що можуть працювати з більш загальним класом задач і з задачами, що можуть бути вирішені лише чисельно (наприклад, знаходження коренів поліноміального рівняння високого ступеню), але при цьому розв’язані гарантовано. Відмітимо, що звичайні чисельні методи зі статичним пошуком(Монте-Карло) або підлаштуванням сітки не можуть бути використані для доведення навіть таких простих властивостей, як пустота і неоднозв’язність множини.

Окрім цього інтервальні методи знайшли широке застосування в моделюванні різноманітних систем, робастному аналізі.

 

9.1 Класична інтервальна арифметика

 

Інтервальну арифметику можна визначити наступним чином:

(3.1)

де . При цьому, якщо означає ділення, то . Неважко показати, що ці операції в кожному конкретному випадку еквівалентні наступним:

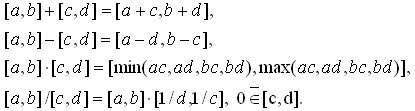     (3.2)

Окрім того, з формули (3.2) слідує, що:

1) віднімання не зворотне додаванню;

2) ділення не зворотне множенню;

3) інтервальне додавання і інтервальне множення асоціативні і комутативні;

4) закон дистрибутивності не виконується, а виконується включення А(В+С) Í  АВ+АС, що називається властивістю субдистрибутивності.

Додавання і множення володіють звичайними властивостями асоціативності і комутативності:

A+(B+C)=(A+B)+C, A×(B×C)=(A×B) ×C,

A+B=B+A, A×B=B×A.

Нулем додавання є число 0, а одиницею множення – число 1:

0+А=А+0=А, 1×А=А×1=А.

Однією з властивостей інтервальної арифметики є мотонність по включенню. Це означає, що з А Í С і В Í D випливає при

Згідно визначення інтервальної арифметики та відповідно до символіки, що є загальною для робіт з інтервального аналізу, наведемо певні додаткові позначення:

а = [; ] – певний інтервал з множини ІR, який ныжньою границею якого є, а верхньою – , тобто ;

|а| = – – довжина інтервалу, легко бачити, що |а| ? 0.

Далі ми будемо позначати через маленьку не потовщену літеру х - дійсний аргумент дійсної функції, х R, а черезвелику літеру Х - інтервальний аргумент інтервальної функції, ХІR;

Будь-яке дійсне число b, може бути представлене в вигляді інтервалу а =[; ],

для якого вірні співвідношення:

b==,

|а| =-=0.

Крім наведених базових арифметичних операцій, можна навести правило розрахунку значення інтервалів, що є результатом ступеню:

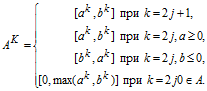(3.3)

та правило помноження інтервалу на дійсну константу:

, (3.4)

Однією з важливих та визначальних властивостей при виконанні операцій в інтервальній арифметиці є властивість вкладення. Формально ця властивість, визначається наступним чином. Якщо інтервали представляють будь-яке фіксоване дійсне число в своєму діапазоні, то і результат арифметичної операції представляє будь-яке можливе дійсне число в діапазоні інтервалу. В символьному запису, така властивість наводиться наступним чином.

Одновимірна функція g^IR має властивість вкладення якщо:

 

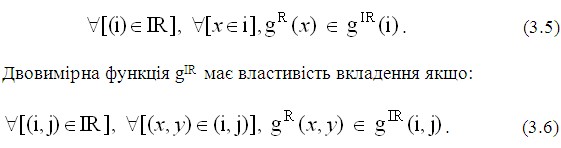
На основі основних алгебраїчних операцій та властивостей інтервального обчислення можна отримати набір елементарних функцій для інтервальних чисел.