
10.14 Застосування активних експериментів при ідентифікації моделей
Перевагою пасивних методів перед активними є те, що при їх використанні не потребується спеціального втручання в хід технологічного процесу. (Питання використання методів інтерполяції і апроксимації при обробці даних пасивних експериментів докладно розглянуті в попередній главі.) Але ця перевага не компенсує недостатньої вірогідності математичних моделей, що отримуються. Тому в моделюванні розвинувся спеціальний напрямок – планування активного експерименту, що дозволяє ефективно використовувати наявні експериментальні ресурси .
Успішне проведення експерименту значною мірою залежить від правильного вибору плану експерименту, який також визначає статистичний аналіз результатів. Вибір методу аналізу залежить від алгебраїчної моделі, що придатна до різних методів обробки даних, і від відомого або припустимого розподілу ймовірностей похибок вимірювань.
Як і в пасивному, в активному експерименті геометричним образом сукупності незалежних змінних ![]() і залежної змінної
і залежної змінної ![]() є простір
є простір ![]() -го виміру, де
-го виміру, де ![]() – число незалежних змінних;
– число незалежних змінних; ![]() -й вимір стосується
-й вимір стосується ![]() . В цьому просторі залежності
. В цьому просторі залежності ![]() від
від ![]() відповідає
відповідає ![]() -мірна поверхня, яку називають поверхнею відгуку (результат досліду розглядається як відгук системи на задану сукупність незалежних змінних або входів).
-мірна поверхня, яку називають поверхнею відгуку (результат досліду розглядається як відгук системи на задану сукупність незалежних змінних або входів).
План експерименту вказує розташування дослідних точок в ![]() -мірному просторі незалежних змінних (або умови всіх дослідів, що їх треба провести). Найчастіше план експерименту задається в вигляді матриці планування – прямокутної таблиці, кожний рядок якої відповідає умовам певного досліду, а
-мірному просторі незалежних змінних (або умови всіх дослідів, що їх треба провести). Найчастіше план експерименту задається в вигляді матриці планування – прямокутної таблиці, кожний рядок якої відповідає умовам певного досліду, а ![]() стовпців – значенням однієї з незалежних змінних в різних дослідах. В
стовпців – значенням однієї з незалежних змінних в різних дослідах. В ![]() -му стовпці наводяться одержані в дослідах значення залежної змінної. Приклад матриці планування експерименту наведено в таблиці 5.1:
-му стовпці наводяться одержані в дослідах значення залежної змінної. Приклад матриці планування експерименту наведено в таблиці 5.1:
Таблиця 5.1
Приклад матриці планування експерименту
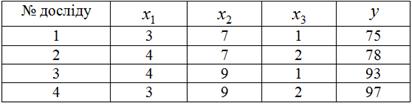
Тут в чотирьох дослідах досліджується вплив на вихід у трьох факторів-входів: ![]() ,
, ![]() і
і ![]() .
.
При одній незалежній змінній план спрощений і найчастіше зводиться до рівномірного розподілу точок через рівні інтервали. В разі більш ніж трьох змінних ![]() план ускладнюється, і при його побудові прагнуть одержати деякі оптимальні властивості:
план ускладнюється, і при його побудові прагнуть одержати деякі оптимальні властивості:
Найбільше розповсюджений такий порядок побудови планів: на першому етапі вибирається центр досліджуваної області (центр плану) і в нього переноситься початок координат; вибирається інтервал варіювання по кожній змінній – відстань по даній осі від центра до експериментальної точки. Вибір центра плану і інтервалу варіювання лежить поза математичною теорією. Цей етап повинен вирішуватись експериментатором на підставі знання об’єктів.
На наступному етапі здійснюють операцію приведення (кодування) змінних. Вона полягає в тому, що всі координати центра плану порівнюють з нулем, а інтервали варіювання ![]() по кожній змінній приймають за одиницю. Кодовані змінні зручні тому, що вся обробка результатів дослідів проводиться в стандартній формі, яка не залежить від конкретних умов задачі; це істотно спрощує обчислення. Перехід від некодованих (натуральних) значень змінних
по кожній змінній приймають за одиницю. Кодовані змінні зручні тому, що вся обробка результатів дослідів проводиться в стандартній формі, яка не залежить від конкретних умов задачі; це істотно спрощує обчислення. Перехід від некодованих (натуральних) значень змінних ![]() до кодованих
до кодованих ![]() і назад відбувається за формулою:
і назад відбувається за формулою:
![]()
і відповідно
![]() ,
,
де ![]() – координата центра плану по j змінній. Розглянемо в наведених координатах найбільше поширений план 1-го порядку для двох незалежних змінних
– координата центра плану по j змінній. Розглянемо в наведених координатах найбільше поширений план 1-го порядку для двох незалежних змінних ![]() і
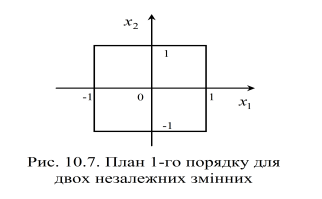
і ![]() . Розташування точок показано на рисунку 5.7. Точки розташовуються у вершинах квадрата, центр О якого збігається з центром плану, сторони паралельні осям і дорівнюють 2. Матриця планування має такий вигляд (табл. 5.2):
. Розташування точок показано на рисунку 5.7. Точки розташовуються у вершинах квадрата, центр О якого збігається з центром плану, сторони паралельні осям і дорівнюють 2. Матриця планування має такий вигляд (табл. 5.2):
Таблиця 5.2
Приклад матриці планування експерименту
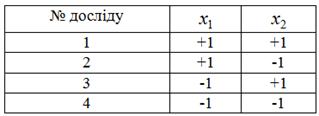
На практиці для скорочення запису часто замість "+1", "-1" пишуть "+", "-". Тоді матриця планування 1-го порядку буде мати вигляд (табл. 5.3):
Таблиця 5.3
Приклад матриці планування експерименту
№ досліду |
|
|
1 |
+ |
+ |
2 |
+ |
- |
3 |
- |
+ |
4 |
- |
- |
Основні особливості і властивості даного плану:
1. План побудований таким чином, що кожна незалежна змінна набуває в дослідах тільки два значення (+1 чи -1), тобто варіюється на двох рівнях (верхньому і нижньому). При цьому в чотирьох дослідах присутні всі можливі парні комбінації цих рівнів обох змінних. Чотири досліди, що поставлені за таким планом, називають повним факторним експериментом (ПФЕ) на двох рівнях для двох факторів; скорочено позначається ПФЕ ![]() .
.
2. При проведенні дослідів за планом ПФЕ розрахунок коефіцієнтів рівняння методом найменших квадратів спрощується, причому з цих дослідів можна знайти коефіцієнти не тільки лінійного рівняння регресії, але й такого, що містить ще один член;
3. Оптимальність використання експериментальних ресурсів: при заданих точності експерименту, кількості дослідів і межах вимірів факторів рівняння регресії виявляється більш точним, ніж те, що одержується з експерименту з іншим розташуванням точок, що досліджуються.
4. Важлива особливість плану – некорельованість факторів. Вона базується на ортогональності матриці планування. Всі стовпці матриці планування (і весь план в цілому) ортогональні. З ортогональності однозначно випливає взаємна незалежність (некорельованість) всіх факторів і, відповідно, всіх коефіцієнтів рівняння регресії.
Вибір матриці планування у вигляді повного факторного експерименту при використанні в якості моделі полінома першого степеня забезпечує оптимальне планування на підставі таких властивостей: всі розрахунки і обчислення проводяться просто; коефіцієнти регресії визначаються незалежно один від одного; дисперсії всіх коефіцієнтів регресії рівні і мінімальні; дисперсія вихідного параметра не залежить від обертання системи координат в центрі плану, а тільки від радіуса досліджуваної сфери факторного простору (властивість рототабельності).
Правильний вибір центра експерименту, інтервалів і рівнів варіювання факторів має вирішальне значення для достовірності побудованої математичної моделі. Основна вимога до інтервалу варіювання полягає в тому, щоб він не був меншим за подвійну квадратичну похибку фактора. Ця вимога пов’язана з тим, що інтервал між двома сусідніми рівнями повинен значно впливати на вихідний параметр. Звичайно інтервал варіювання вибирається на підставі апріорної інформації і потім уточнюється після одержання математичної моделі. Вдалий вибір інтервалу варіювання факторів гарантує достовірність математичної моделі об’єкта. Якщо інтервал варіювання вибраний невдало і модель неадекватна, то для уточнення моделі необхідно повторити експерименти.
Важливим елементом розробки плану експерименту є вибір числа рівнів для кожного фактора. Найбільше розповсюдження одержало планування факторів на двох рівнях, коли в якості рівнів використовуються верхня і нижня межі інтервалу варіювання. Постановка експериментів за такими планами називається дворівневим повним факторним експериментом типу ![]() , де
, де ![]() – число факторів. Тоді для двох факторів число експериментів
– число факторів. Тоді для двох факторів число експериментів ![]() , для трьох
, для трьох ![]() і т.д.
і т.д.
Розглянемо побудову матриці планування для повного факторного експерименту при трьох факторах (ПФЕ, ![]() ). Щоб перебрати всі комбінації для трьох факторів на двох рівнях, випишемо два рази комбінації для двох факторів (ПФЕ,
). Щоб перебрати всі комбінації для трьох факторів на двох рівнях, випишемо два рази комбінації для двох факторів (ПФЕ, ![]() ), один раз в сполученні зі значенням
), один раз в сполученні зі значенням ![]() , другий - з значенням
, другий - з значенням ![]() (рисунок 5.8). Виходить такий план (матриця ПФЕ,
(рисунок 5.8). Виходить такий план (матриця ПФЕ, ![]() ):
):
Таблиця 5.4
Приклад побудови матриці планування для повного факторного експерименту

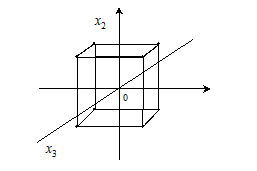
Рисунок 5.8 – Матриця планування для повного факторного експерименту
Приклад розробки математичної моделі за результатами активного експерименту розглянуто у Додатку А.
Дробовий факторний експеримент (ДФЕ)
Дворівневий план ефективний (особливо при ![]() ), коли для перевірки адекватності моделі мають достатню кількість степенів вільності, тобто є перевищення числа дослідів
), коли для перевірки адекватності моделі мають достатню кількість степенів вільності, тобто є перевищення числа дослідів ![]() над числом коефіцієнтів моделі
над числом коефіцієнтів моделі ![]() , що визначаються. Число
, що визначаються. Число ![]() визначає об’єм вибірки при повному факторному експерименті. При певній постановці задачі іноді параметри доводиться варіювати не на двох, а на більшій кількості рівнів. Якщо число потрібних рівнів позначити через
визначає об’єм вибірки при повному факторному експерименті. При певній постановці задачі іноді параметри доводиться варіювати не на двох, а на більшій кількості рівнів. Якщо число потрібних рівнів позначити через ![]() , то об’єм повного факторного експерименту визначиться виразом
, то об’єм повного факторного експерименту визначиться виразом ![]() . Великий об’єм вибірки дає можливість точно визначити коефіцієнти моделі і мати достатньо степенів вільності для перевірки адекватності моделі. Але це призводить до великих експериментальних і обчислювальних робіт. Наприклад, якщо в чотирифакторному експерименті фактори
. Великий об’єм вибірки дає можливість точно визначити коефіцієнти моделі і мати достатньо степенів вільності для перевірки адекватності моделі. Але це призводить до великих експериментальних і обчислювальних робіт. Наприклад, якщо в чотирифакторному експерименті фактори ![]() і
і ![]() мають по два рівні, фактор
мають по два рівні, фактор ![]() – три і фактор
– три і фактор ![]() – чотири рівні, то число точок плану дорівнює
– чотири рівні, то число точок плану дорівнює ![]() .
.
При збільшенні числа факторів і числа рівнів кожного фактора істотно зростає число точок плану, що створюють повну факторну решітку. Наприклад, якщо б кожний з семи факторів в деякому модельному прикладі мав тільки два рівні, то для побудови повного факторного плану було б потрібно ![]() точок. Таким чином, повний факторний план приводить до надмірних витрат часу і засобів.
точок. Таким чином, повний факторний план приводить до надмірних витрат часу і засобів.
В разі неповного дослідження (наприклад, дослідження лише головних ефектів і двофакторних взаємодій без розгляду взаємодій більш високого порядку) використовують неповні факторні плани, які дозволяють розв’язати поставлену задачу і потребують меншої кількості дослідів порівняно з повним факторним планом.
В будь-якому плані з числом дослідів, меншим, ніж у повного факторного плану, присутні ефекти змішування.
Звичайно в ході експерименту цікавими є головні ефекти, і важливо, щоб вони не змішувались між собою. Практично в усіх неповних факторних планах, що застосовуються, головні ефекти змішуються лише з ефектами взаємодії високого порядку. Таким чином, при оцінці головних ефектів за допомогою цих планів припускається (в крайньому разі, попередньо), що взаємодії, які можуть змішуватися з головними ефектами, дорівнюють нулю або достатньо малі.
Кількість експериментів можна скоротити, якщо заздалегідь домовитись про структуру моделі. Припустимо, для задачі, що досліджується, достатньо мати лінійну модель об’єкта. Тоді в разі наявності трьох змінних повний факторний експеримент дозволяє знайти вільний член, три коефіцієнти при лінійних членах і чотири степені вільності для перевірки адекватності. При ![]() загальний об’єм експериментів дорівнює 64, з них сім експериментів використовується для визначення вільного члена і коефіцієнтів при лінійних членах, а 57 – для перевірки адекватності моделі. В цьому випадку, як ми бачимо, є надлишок інформації для знаходження адекватності моделі процесу. При цьому доцільно ставити не всі
загальний об’єм експериментів дорівнює 64, з них сім експериментів використовується для визначення вільного члена і коефіцієнтів при лінійних членах, а 57 – для перевірки адекватності моделі. В цьому випадку, як ми бачимо, є надлишок інформації для знаходження адекватності моделі процесу. При цьому доцільно ставити не всі ![]() експериментів, а менше, в залежності від вибраного числа степенів вільності визначення адекватності моделі і від вибраної структурі моделі. Зменшити число експериментів можна, якщо прирівняти рівні однієї або декількох змінних добутку рівнів інших змінних, коли їх мінімальні і максимальні рівні прийняті, відповідно, за -1 і +1.
експериментів, а менше, в залежності від вибраного числа степенів вільності визначення адекватності моделі і від вибраної структурі моделі. Зменшити число експериментів можна, якщо прирівняти рівні однієї або декількох змінних добутку рівнів інших змінних, коли їх мінімальні і максимальні рівні прийняті, відповідно, за -1 і +1.
Нехай є чотири змінних. Повний факторний експеримент для такої кількості змінних дорівнює 16. Для лінійної структури моделі достатньо п’яти експериментів. При цьому рівень четвертої змінної можна брати за знаком добутку перших трьох змінних, тобто ![]() , де
, де ![]() ,
, ![]() ,
, ![]() можуть приймати значення -1 чи +1. Якщо перший експеримент ставиться таким чином, що перша змінна знаходиться на нижньому рівні, тобто дорівнює -1, друга також на нижньому рівні, а третя - на верхньому, то четвертий параметр ставиться на верхній рівень. Число експериментів в такому випадку скорочується до восьми. Вісім експериментів достатньо для визначення вільних членів, коефіцієнтів при лінійних членах і для оцінки адекватності моделі.
можуть приймати значення -1 чи +1. Якщо перший експеримент ставиться таким чином, що перша змінна знаходиться на нижньому рівні, тобто дорівнює -1, друга також на нижньому рівні, а третя - на верхньому, то четвертий параметр ставиться на верхній рівень. Число експериментів в такому випадку скорочується до восьми. Вісім експериментів достатньо для визначення вільних членів, коефіцієнтів при лінійних членах і для оцінки адекватності моделі.
Такий план називається дробовою реплікою (ДР) від повного факторного експерименту. В залежності від постановки задачі повний факторний експеримент можна скорочувати до дробових реплік різного розміру. При наявності семи параметрів повний факторний експеримент ![]() , наприклад, можна скоротити до дробової репліки розміру
, наприклад, можна скоротити до дробової репліки розміру ![]() , якщо прийняти, що
, якщо прийняти, що ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
В загальному випадку при наявності ![]() параметрів і скороченні повного факторного експерименту на
параметрів і скороченні повного факторного експерименту на ![]() ступенів вийде дробовий факторний експеримент об’ємом
ступенів вийде дробовий факторний експеримент об’ємом ![]() .
.
Для побудови дробових реплік використовують спеціальні алгебраїчні вирази, які полегшують виявлення змішаних ефектів. Їх називають генерувальними співвідношеннями чи визначальними контрастами. Генерувальним називається співвідношення, що показує, які взаємодіючі фактори замінені новими (воно генерує, або створює ДР). Так, вищерозглянуте планування типу ![]() (піврепліка від
(піврепліка від ![]() ), що задавалось одним з таких генерувальних співвідношень:
), що задавалось одним з таких генерувальних співвідношень: ![]() або
або ![]() .
.
З генерувальними співвідношеннями можна проводити алгебраїчні операції: множити обидві частини рівняння на будь-які ефекти - лінійні, подвійні, потрійні та інші взаємодії. При цьому фактор, що піднесений до квадрату або до іншого парного степеня, замінюють одиницею (![]() ). Помноживши генерувальні співвідношення для плану
). Помноживши генерувальні співвідношення для плану ![]() на
на ![]() , одержуємо
, одержуємо![]() ;
; ![]() , або, якщо врахувати на те, що сказано вище,
, або, якщо врахувати на те, що сказано вище, ![]() ;
; ![]() .
.
Такі добутки називають визначальним контрастом. Визначальний контраст дає можливість встановити розв’язувальну здатність дробової репліки, тобто знайти, які з коефіцієнтів є незмішаними оцінками факторів. За прийнятим визначальним контрастом одержують співвідношення, які задають змішані оцінки для даної дробової репліки. Для цього кожний фактор множать на визначальний контраст.
Коефіцієнти рівняння регресії для ПФЕ і ДР визначаються за однаковими формулами. При використанні вимірних змінних ![]() переходять до безвимірних (нормованих) змінних:
переходять до безвимірних (нормованих) змінних:
![]() .
.
Тут ![]() визначені через змінну на вихідному (основному) рівні +1. Для повних факторних планів (ПФП) і їх ДР
визначені через змінну на вихідному (основному) рівні +1. Для повних факторних планів (ПФП) і їх ДР
![]()
![]() ;
;
![]() ;
;
![]() .
.
При використанні нормованих змінних спрощується розрахунок коефіцієнтів ![]() і їх дисперсії. Для ПФП і ДР знаходимо
і їх дисперсії. Для ПФП і ДР знаходимо
![]()
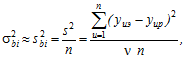
де надійний інтервал ![]() .
.
Наведені співвідношення характеризують нормалізоване рівняння регресії ![]() .
.
Активна ідентифікація нелінійних моделей
Якщо математична модель процесу нелінійна, то, як і при пасивних методах, вона апроксимується поліномом. Однак при одержанні математичної моделі кількість необхідних дослідів при зростанні числа членів цього полінома швидко зростає. В зв’язку з цим потрібно інакше розв’язувати питання про число рівнів, центр плану експерименту і принципи оптимальності планів, що застосовуються. Розв’язок цих питань здійснюється різними методами. Найбільш в інженерній практиці для опису нелінійної області використовуються методи центрального композиційного рототабельного і ортогонального планування. При плануванні за допомогою цих методів необхідно перш за все вибрати нульову точку, число рівнів і принцип оптимальності.
За нульову точки приймається центр плану, що вже був використаний раніше (наприклад, ПФЕ), який дає неадекватну лінійну модель (значущими виявляються ефекти взаємодії і квадратичні). При цьому проведені експерименти доповнюються спеціальними дослідами (такі плани називаються центральними композиційними). При використанні математичної моделі в вигляді полінома другого порядку двома рівнями варіювання факторів обмежуватись не можна. Але плани на трьох рівнях неекономічні з точки зору кількості дослідів. Якщо доповнити дворівневий план ПФЕ визначеними точками факторного простору, можна одержати оптимальний план. Ядро центрального композиційного плану складає ПФЕ типу ![]() при
при ![]() . Якщо
. Якщо ![]() , то користуються дробовими репліками, які забезпечують роздільне визначення лінійних ефектів і ефектів взаємодії. План ПФЕ доповнюють деякою кількістю зіркових точок, координати яких залежать від прийнятого принципу оптимальності. Загальна кількість дослідів при такому плануванні визначається формулою
, то користуються дробовими репліками, які забезпечують роздільне визначення лінійних ефектів і ефектів взаємодії. План ПФЕ доповнюють деякою кількістю зіркових точок, координати яких залежать від прийнятого принципу оптимальності. Загальна кількість дослідів при такому плануванні визначається формулою ![]() де доданки – відповідно, число дослідів ПФЕ, зіркових і нульових точок.
де доданки – відповідно, число дослідів ПФЕ, зіркових і нульових точок.
Розглянемо побудову найбільш розповсюдженого типу планів другого порядку – центрального композиційного плану: центральні – внаслідок симетричності відносно центра плану, композиційні – оскільки вони компонуються додаванням визначеного числа дослідів до плану 1-го порядку. В цьому велика перевага таких планів: якщо рівняння 1-го порядку неадекватно описує об’єкт, то не треба ставити всі досліди заново, а достатньо додати точки – добудувати план до плану 2-го порядку, як показано на рисунок 5.9 (![]() ).
).
До точок повного факторного експерименту додаються точки в центрі плану (одна або декілька паралельних) і точки, що розташовані на всіх осях координат на відстанях ![]() від центра. Точки на осях називають зірковими точками, а величину
від центра. Точки на осях називають зірковими точками, а величину ![]() – зірковим плечем. Для різних планів зіркове плече може бути різним.
– зірковим плечем. Для різних планів зіркове плече може бути різним.
Матриця такого плану для двох незалежних змінних (план 2-го порядку при ![]() ) має вигляд:
) має вигляд:
Таблиця 5.5
Приклад матриці планування експерименту

* – зіркова точка; ** – центральна точка.
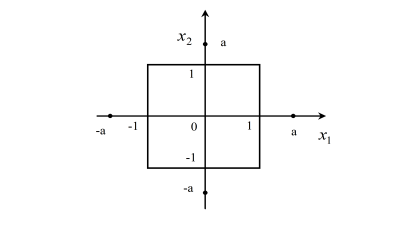
Рисунок 5.9 – Центральний композиційний план
Загальне число точок плану 2-го порядку дорівнює ![]() , де
, де ![]() – число зіркових точок,
– число зіркових точок, ![]() – число точок в центрі. Якщо план 1-го порядку – дробовий, то число точок плану 2-го порядку дорівнює
– число точок в центрі. Якщо план 1-го порядку – дробовий, то число точок плану 2-го порядку дорівнює ![]() .
.
При рототабельному плануванні і повному факторному експерименті зіркове плече ![]() ; для дробового факторного експерименту
; для дробового факторного експерименту ![]() , де
, де ![]() – дробовість репліки (
– дробовість репліки (![]() - піврепліка,
- піврепліка, ![]() – чверть репліки і т.д.).
– чверть репліки і т.д.).
Для вибору зіркового плеча, числа зіркових і нульових точок користуються даними таблиці 5.6:
Таблиця 5.6
Дані для вибору зіркового плеча, числа зіркових і нульових точок
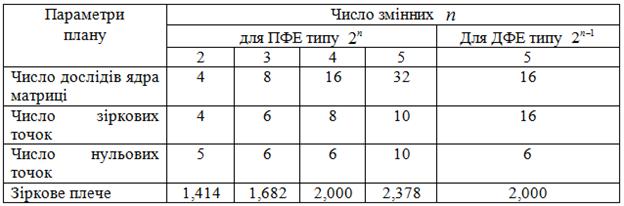
При рототабельному плануванні завдяки експериментальним точкам в центрі плану дисперсія передбачуваного значення всередині області експериментування постійна і не залежить від відстані до центра плану.
При обробці планів 2-го порядку потрібен значний об’єм обчислень, що виконують на ЕОМ.
При ортогональному плануванні до факторного експерименту або дробової репліки додають ![]() дослідів (
дослідів (![]() – число змінних), причому один з них – "центральний" (
– число змінних), причому один з них – "центральний" (![]() ), а в
), а в ![]() – "зіркові". В "зіркових" дослідах кожна з нормованих змінних по черзі приймає значення
– "зіркові". В "зіркових" дослідах кожна з нормованих змінних по черзі приймає значення ![]() , а для решти змінних заданий основний рівень (
, а для решти змінних заданий основний рівень (![]() ). При кількості змінних
). При кількості змінних ![]() значення
значення ![]() відповідно дорівнюють 1; 1,215 і 1,414.
відповідно дорівнюють 1; 1,215 і 1,414.
За результатами ортогонального планування визначають коефіцієнти рівняння регресії:
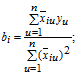
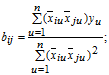
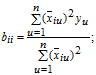
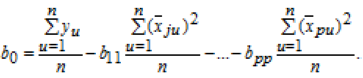
В ході оцінки адекватності при рототабельному і ортогональному плануванні розрахункове значення критерію Фішера визначають як відношення дисперсії адекватності до дисперсії досліду:
![]()
і порівнюють з табличним ![]() для степенів вільності
для степенів вільності ![]() і
і ![]() .
.
Контрольні запитання та завдання
1. Сформулюйте класичну постановку задачі оптимізації.
2. В чому полягає задача оптимального проектування?
3. За якими ознаками класифікуються задачі оптимізації?
4. Яка задача дістала назву математичного програмування?
5. Які особливості мають задачі нелінійного, стохастичного, динамічного, квадратичного, сепарабельного, геометричного програмування?
6. Чим відрізняються задачі багатопараметричної і багатокритеріальної оптимізації?
7. Сформулюйте умови стаціонарності для задачі гладкої оптимізації.
8. Запишіть та поясніть умови Куна - Такера.
9. Дайте характеристики та порівняйте чисельні методи розв’язання задачі гладкої оптимізації.
10. Спробуйте розв’язати задачу оптимізації іншими методами, окрім методу градієнтного спуску.
11. Як звести загальну задачу оптимізації до задачі без обмежень?
12. Які існують методи опуклої оптимізації?
13. Зробіть постановку задачі лінійного програмування. В яких випадках вона не має розв’язку?
14. Дайте характеристику методу розгалужень і меж розв’язання задачі лінійної оптимізації.
15. В яких випадках і як застосовується теорія ігор для розв’язання задач дискретної оптимізації? Як вибирається стратегія гравця?
16. Сформулюйте принципи оптимізації Беллмана.
17. Яку задачу називають задачею комівояжера?
18. Складіть програми пошуку найкоротшого шляху в графах з ребрами одиничної та довільної довжини.
19. Чим відрізняються активні та пасивні експерименти?
20. Що таке план експерименту? Як він задається? Чим відрізняються дробовий та повний факторні експерименти?
21. Як розраховуються коефіцієнти рівняння регресії?
Як визначити необхідну кількість випробувань при проведенні активних експериментів.