10.4     Гладка оптимізація

 

У випадку, коли функція цілі і функції , які задають обмеження, є диференційними (гладкими), для розв’язання задач оптимізації використовується поняття градієнта. Для будь-якої функції , що диференціюється, її градієнтом в точці називається вектор

.

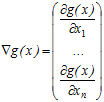Вектор градієнта задає (в даній точці ) напрям найшвидшого росту функції , а зворотний йому напрям , що називається антиградієнтом, напрям найшвидшого спадання цієї функції. Точки, в яких градієнт функції перетворюється в нуль, називаються її стаціонарними точками. Якщо екстремум функції досягається всередині припустимої області (не на її межі), то в точці оптимуму її градієнт перетворюється в нуль, тобто має місце система рівнянь

Ці рівняння (умови стаціонарності функцій) мають місце не тільки для абсолютних, але й для локальних екстремумів. Разом з тим умови стаціонарності не є достатніми.

 

10.4.1 Умови Куна-Таккера

 

У випадку, коли екстремальна точка лежить на межі припустимої множини, вона не обов’язково є стаціонарною. Але за деякої додаткової умови може, якщо замінити цільову функцію так званою функцією Лагранжа (де – ліві частини всіх граничних умов), дістати того, щоб граничні екстремальні точки функції були стаціонарними точками функції Лагранжа при відповідних значеннях параметрів .

Умова, про яку йдеться, є так званою умовою регулярності – виконується на практиці. Вона полягає в лінійній незалежності в даній точці градієнтів всіх мережних функцій , для яких .

При виконанні цієї умови для будь-якої точки максимуму в задачі “знайти mах при , ” і для будь-якої точки мінімуму в задачі “знайти min при , ” повинні виконуватися такі три умови, які називаються умовами Куна-Таккера:

1)  лежить в припустимій множині;

2)  при ;

3) .

де – деякі дійсні числа (множники Лагранжа), довільні для всіх умов типу рівності і невід’ємні для всіх умов типу нерівності .

 

10.4.2 Чисельні методи гладкої оптимізації

 

Метод оптимізації, який використовує умови Куна-Таккера, на практиці застосовується відносно рідко через велику складність аналізу системи співвідношень, що виникає. Найчастіше застосовуються чисельні методи оптимізації, для яких достатньо вміти знаходити чисельні значення градієнта в будь-якій заданій точці.

Загальна ідея методу градієнтного спуску (підйому)

Нехай неперервно диференційована цільова функція задана в усіх точках простору . Вирішуючи від точки на дуже малий крок в будь-якому напрямку , де – одиничний вектор, в силу умови диференційованості функції , одержимо нерівності:

Це означає, що рух (на дуже малий крок) в напрямку градієнта функції забезпечує найбільший підйом, а в напрямку антиградієнта – найбільше спадання цієї функції. Ці напрямки називають відповідно напрямком найшвидшого підйому і найшвидшого спуску функції в даній точці .

Виходячи з заданої точки , будуємо послідовність точок так, що переміщення від кожної точки до наступної точки проводиться в напрямку найшвидшого підйому (при пошуку максимуму) або найшвидшого спуску (при пошуку мінімуму).

Важкість практичного застосування такої процедури полягає перш за все у виборі величини кроку при переході від точки до точки . Справа в тім, що нерівності мають місце лише в малому околі точки , тобто для малої величини кроку . При великому значенні кроку можна, прямуючи в напрямку найшвидшого підйому, одержати не збільшення, а зменшення значення цільової функції . Те ж саме має місце і для процедури спуску.

Отже, величину кроку в процедурах найшвидшого підйому і спуску необхідно вибирати достатньо малою. Проте при прямуванні малими кроками для наближення до екстремальної точки може знадобитись дуже велика кількість кроків. Крім того, від процедур підйому і спуску звичайно потребується не просто наближення до екстремальної точки , а збіжність до неї. Це означає, що зі збільшенням кількості кроків відстань від точки до точки екстремуму повинна наближатися до нуля. Це можливо лише в тому випадку, якщо з наближенням до точки екстремуму величина кроку буде наближатись до нуля. На рисунку 5.2 наведений алгоритм пошуку екстремуму функції за методом градієнтного спуску.

Пропорційно - градієнтний метод

Найбільш простим способом забезпечення необхідного зменшення кроку при наближенні до точки екстремуму для диференціальної функції є вибір довжини кроку пропорційним довжині вектора градієнта в точці :

Такий вибір кроку означає, що перехід від точки до точки буде виконуватись за формулою для процедури підйому (знаходження максимуму функції ) і за формулою для процедури спуску (знаходження мінімуму функції ).

Повнокроковий градієнтний метод

В цьому методі кожний крок градієнтного підйому або спуску виконується максимально можливої довжини, яка забезпечує необхідний напрямок зміни значення функції (тобто її збільшення або зменшення). Інакше кажучи, на напівпрямій, що виходить з чергової точки в напрямку градієнта (при підйомі) або антиградієнта (при спусканні) відшукується точка абсолютного максимуму або мінімуму, яка і вибирається як наступна точка .

В випадку довільної диференціальної функції розв’язання подібної задачі, що її називають одновимірною оптимізаційною задачею, спрощується при накладанні на функцію деяких додаткових вимог, наприклад, опуклості.

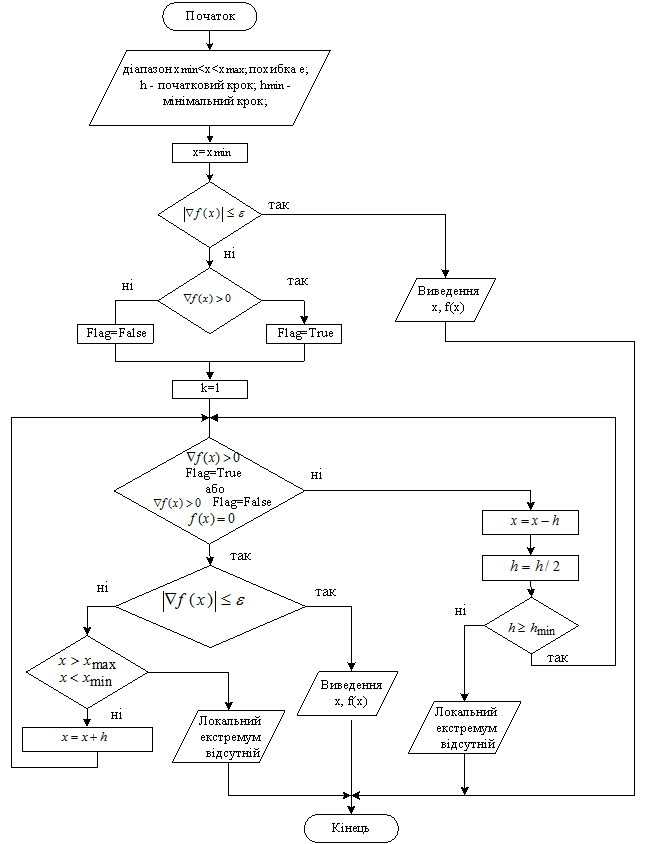
Рисунок 5.2 – Алгоритм методу градієнтного спуску (підйому)

 

Метод спряжених градієнтів

Для випадку, коли функція – квадратний поліном, розроблена точна процедура, при повних кроках якої точки екстремуму досягаються з будь-якої початкової точки за кроків (де – розмірність простору). Напрямок кроку від точки до точки задається в цьому методі такою рекурентною формулою:

де означає довжину вектора .

Знак плюс вибирається в тому випадку, коли розглядається задача максимізації, а знак мінус – у випадку розв’язання задачі мінімізації. Такий же вибір знака здійснюється і для напрямку першого кроку . Воно збігається з напрямком

 

10.4.3 Методи зведення загальної задачі оптимізації до задачі без обмежень

 

Чисельні методи гладкої оптимізації, які описані вище, в чистому вигляді застосовуються звичайно для задач без обмежень. Задачі загального вигляду (тобто задачі з обмеженнями) зводять до задач без обмежень за рахунок зміни цільової функції. Нехай, наприклад, потрібно знайти максимум функції при обмеженнях В так званому методі штрафних функцій будується функція , яку називають штрафною функцією, і яка всередині припустимої області приймає нульове значення, а поза нею – від’ємне. Найчастіше в якості такої функції вибирають функцію вигляду

,

після чого будують послідовність додатних чисел яка збігається до нуля.

При заміні цільової функції функцією

розв’язують задачу без обмежень для цієї функції, починаючи з . Якщо розв’язок належить припустимій області, тобто якщо всі , то є розв’язком початкової задачі з обмеженням. В протилежному випадку замінюють на і розв’язують задачу для нової цільової функції .

Алгоритм розв’язання такої задачі наведений на рисунку 5.3.

В методі бар’єрів при розв’язанні задачі max при цільову функцію замінюють функцією , де бар’єрна функція характеризується властивістю прямувати до при наближенні до границі припустимої області зсередини. Таку функцію можна задати, наприклад, формулою:

,

якщо область задана нерівностями .

Таким же чином, як і в методі штрафних функцій, вибирають послідовність додатних чисел яка збігається до нуля. Розв’язуються задачі без обмежень для цільових функцій при

Якщо при цьому використовується той або інший чисельний метод, в якому початкова точка вибирається всередині то наявність бар’єра забезпечить належність екстремальної точки (при її існуванні) області Наявність екстремуму забезпечується умовами обмеженості в області і неперервності функцій і .