10.6 Негладка оптимізація за методом координатного спуску (підйому)

 

При оптимізації недиференційованих функцій можна відмовитись від будь-яких узагальнень понять градієнта та використовувати лише кроки вздовж осей координат. З цією метою досліджують значення цільової функції на черговому кроці оптимізації з приростом однієї з координат і переходять від точки до точки . Знак приросту вибирають таким чином, щоб значення функції змінювалось в потрібному напрямку (збільшувалось при максимізації і зменшувалось при мінімізації). Величини вибирають звичайно як в покрокових методах та забезпечують максимально можлива зміна функції в обраному напрямку.

Зсуви здійснюються по черзі по всіх осях координат, причому після зсуву по останній осі знову повертаються до першої осі . Якщо повторити цей процес достатньо багато разів, як правило, можна знайти як завгодно точне наближення деякого екстремуму заданої негладкої функції в тому разі, коли виконується припущення, що такий екстремум існує.

 

10.7 Стохастична оптимізація

 

Іноді корисно замінити зсуви вздовж координатних осей зсувами (з відповідним знаком) вздовж випадково вибраного на кожному кроці напрямку. При достатньо загальних припущеннях внаслідок таких зсувів з імовірністю одиниця за достатньо велике число кроків екстремальна точка може бути апроксимована з будь-яким необхідним ступенем точності. Перевагою методу є простота кожного окремого кроку оптимізації. Проте кількість кроків порівняно з методами, які забезпечують пошук задовільних напрямків руху, у подібних простих методів, як правило, значно більша. При цьому на практиці вони можуть виявитися менш ефективними, ніж більш складні методи, що використовують поняття субградієнта і різні додаткові способи прискорення збіжності.

 

10.8 Лінійне програмування

 

Однією з задач опуклої оптимізації, що найчастіше зустрічаються, є так звана задача лінійного програмування, в якій як цільова функція, так і всі обмеження лінійні. Для розв’язання цієї задачі можуть бути застосовані загальні способи опуклої оптимізації, які описані в п’ятому розділі цієї глави. Але на практиці для цього випадку застосовують інші, більш прості способи, з одним з яких (так званий симплекс-метод) ми зараз ознайомимося.

Постановки задач лінійного програмування, які зустрічаються на практиці, передбачають ще одне додаткове обмеження. Це умова невід’ємності значень всіх змінних. Далі, обмеження типу нерівностей або введенням додаткових змінних з невід’ємними значеннями перетворюються в рівності або . Крім того, простою зміною знака цільової функції задача знаходження максимуму зводиться до задачі знаходження мінімуму. Таким чином, в лінійному програмуванні можна обмежитись лише розв’язанням задачі мінімізації.

Стандартна постановка задачі лінійного програмування полягає в тому, щоб: знайти мінімум лінійної функції при обмеженнях .

Інакше, йдеться про знаходження невід’ємного розв’язку даної системи лінійних алгебраїчних рівнянь , яке перетворює в мінімум значення даної лінійної функції .

Задача лінійного програмування може не мати розв’язку в таких випадках:

1) система рівнянь несумісна, тобто взагалі не має розв’язків;

2) система не має жодного від’ємного розв’язку;

3) на множині невід’ємних розв’язків системи цільова функція може приймати як завгодно великі за абсолютною величиною від’ємні значення, тобто .

 

10.8.1 Симплекс - метод

 

Один з найбільш розповсюджених методів розв’язування задачі лінійного програмування в стандартній постановці полягає в послідовному застосуванні до лінійних функцій так званих симплексних перетворень, що являють собою розв’язки одного з обмежувальних рівнянь відносно деякого невідомого , і підстановку знайденого таким чином значення до всіх обмежувальних рівнянь і в цільову функцію .

 

10.8.2 Транспортна задача

 

В деяких окремих випадках розв’язання задачі лінійного програмування може бути значно спрощено. Найважливішим з таких випадків є так звана транспортна задача, яку називають іноді задачею про призначення. Суть її полягає в мінімізації цільової функції

при обмеженнях типу рівнянь

Звичайно додатково припускається зберігання рівняння

інакше задача не буде мати розв’язків.

Назву транспортної задача, що розглядається, одержала тому, що до неї зводиться оптимізація плану перевезень вантажів з пунктів відправлення з запасами до пунктів призначення з об’ємами споживання . Роль коефіцієнтів в цільовій функції виконують питомі вартості, тобто вартості перевезення однієї одиниці вантажу з пункту в пункт . Задача полягає в мінімізацїї загальної вартості перевезення вантажів за умови, що вантажі повністю вивезені з усіх пунктів відправлення і потреби всіх пунктів призначення виявились повністю задоволеними.

 

10.8.3 Цілочислове лінійне програмування

 

Іноді на практиці доводиться зустрічатися з такими задачами лінійного програмування, в яких припустимі лише цілочислові розв’язки.

В загальному випадку одержання цілочислового розв’язку потребує застосування спеціальних методів, серед яких найчастіше вживають методи відтинань та розгалужень і меж.

Методи відтинань базуються на таких ідеях. Спочатку розв’язується звичайна задача лінійного програмування (з тимчасово відкинутою вимогою цілочислового розв’язку). Якщо координати точки , яка одержана в результаті розв’язання задачі , цілі числа, то ця точка надає розв’язок не тільки задачі , але й початкової задачі цілочислового лінійного програмування, яку ми домовимося позначати через .

Якщо хоча б одна з координат точки , наприклад, , не є цілим числом, то до початкової задачі цілочислового лінійного програмування додається нове обмеження, що побудоване з використанням інформації, яка є в таблиці симплекс-методу і відповідає кроку, на якому побудований розв’язок .

В результаті виходить нова задача , до якої знов застосовується та ж сама процедура. Таким чином, методи відтинань будують і розв’язують послідовність лінійних задач кожна з яких відрізняється від попередньої лише одним новим обмеженням.

 

10.8.4 Загальна задача лінійної оптимізації

 

В загальному випадку задача дискретної оптимізації не припускає лінійності як цільової функції , так і обмежень . Не вимагається також неодмінно цілочисельність координат точок, серед яких знаходиться розв’язок. Важливо лише, щоб вони утворювали дискретну множину . Звичайно на практиці загальне число точок виявляється настільки великим, що простий перебір фізично неможливий навіть при використанні найпотужніших ЕОМ. З цієї причини основна задача в дискретній оптимізації зводиться до розробки методів, які направлені на максимально можливе звуження перебору.

У так званих прямих методах дискретної оптимізації звичайно використовуються ті чи інші аналоги (в неперервному випадку) градієнтних методів, що розглядалися вище. До них відносять методи локальної оптимізації, наприклад, метод вектора спаду. Обчислювальну схему цього методу для розв’язання задачі мінімізації дійсної функції , що визначена на деякому просторі дискретного метричного простору , можна описати таким чином.

Спочатку вибираємо деяке початкове наближення і радіус . В просторі розглядаємо окіл радіуса з центром в точці . Досліджуючи координати вектора спаду, який характеризує зміни значень цільової функції в точках множини порівняно з , визначаємо, чи є точкою локального мінімуму функції . Якщо ні, то за допомогою вектора спаду в множині вибираємо точку , для якої значення цільової функції менше, ніж . На наступній ітерації знову повторюємо цю ж процедуру, виходячи вже з як з центра нового околу, і так далі. Процес обчислень вважається закінченим, якщо одержаний деякий локально оптимальний розв’язок задачі. Алгоритм методу припускає переривання обчислень на будь-якій ітерації з видачею в якості результату останнього одержаного припустимого розв’язку задачі.

В релаксаційних методах звертаються до способу ослаблення (релаксації) обмежень і заміни цільової функції її мінорантою (в задачі мінімізації), тобто функцією, яка задовольняє умову для всіх .

З припустимої області , що здобута розширенням вихідної області за рахунок ослаблення обмежень, і вибираються так, щоб, по-перше, релаксована задача допускала порівняно прості способи розв’язувань, і, по-друге, щоб вона найменше відрізнялась від вихідної за цільовою функцією і множиною припустимих розв’язків:

Метод розгалужень і меж (МРМ)

Цей метод дозволяє отримати точний або наближений розв’язок з заданою відносною похибкою за цільовою функцією. Суть МРМ полягає в тому, що замість вихідної задачі оптимізації будується і розв’язується послідовність релаксованих задач Спочатку розв’язується задача для і , то – оптимальний розв’язок , і процес закінчується. Інакше – оцінка знизу для цільової функції на оптимальному розв’язку задачі , і алгоритм починає процес розгалуження вихідної задачі на декілька задач (безпосередніх нащадків).

 

10.9     Теорія ігор

 

До методів дискретної оптимізації і лінійного програмування часто доводиться звертатись при аналізі і виборі рішень в конфліктних ситуаціях, тобто при наявності сторін, що мають на меті відмінні (найчастіше – протилежні) цілі.

Стратегією гравця називають сукупність правил, що визначають поведінку гравця від початку гри до її завершення.

Задання стратегій двох гравців в парній грі повністю визначає її наслідок, тобто виграш одного і програш другого. Гра називається скінченною, якщо в кожного гравця є лише скінченна кількість стратегій. Результати скінченної парної гри з нульовою сумою можна задавати матрицею, рядки і стовпці якої відповідають відмінним стратегіям, а її елементи - відповідні виграші однієї сторони (які дорівнюють програшам другої).

Розглянемо гру з матрицею

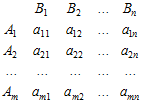
Якщо перший гравець застосовує стратегію , то другий буде прагнути до того, щоб вибором відповідної стратегії звести виграш першого гравця до мінімуму. Величина цього мінімуму, яку ми позначимо , дорівнює, очевидно, .

З точки зору першого гравця (при будь-яких відповідях супротивника) доцільно прагнути знайти таку стратегію, при якій перетворюється в максимум. Цей максимум, який ми позначимо , називається нижньою ціною гри. Оскільки значення обчислюється за формулою , то його називають також максиміном. Йому відповідає максимінна стратегія, дотримуючись якої, перший гравець при будь-яких стратегіях у противника забезпечить собі виграш, який не менше (в залежності від знака це може бути і програш, який в цьому разі виявиться мінімальним).

Аналогічно визначається мінімальний програш (який може бути в дійсності і виграшем) для другого гравця: .

Величина називається верхньою ціною гри або мінімаксом. Їй відповідають мінімаксні стратегії другого гравця.

Має місце нерівність . При розв’язок одержується в чистих стратегіях. Для знаходження їх достатньо виділити в платіжній матриці максимінні (тобто рівні ) елементи. Будь-яка пара рядків і стовпців, на перетині яких знаходиться такий елемент, відповідає парі чистих оптимальних стратегій. При перший гравець може істотно збільшити свій середній виграш порівняно з , якщо він буде користуватись не чистою (однією єдиною) стратегією, а так званою змішаною стратегією. Змішана стратегія полягає в тому, що при повторі гри здійснюється випадковий вибір стратегії з деякої множини змішуваних стратегій, і для кожної змішуваної стратегії вказується імовірність її вибору.