Приклади до розділу 3. Нелінійні задачі

 

Приклад 3.1. Метод графічного відділення коренів.

Розглянемо в якості приклада рівняння x³ – 3x – 0,4 = 0. Запишемо його як

x3 = 3x + 0,4

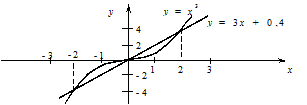
З графіка видно, що тут три корені: с₁ О [–2, –1]; с₂ О [–1, 0]; с₃ О [1, 2].

Приклад 3.2. Методом половинного ділення знайти розв’язок рівняння з точністю 0,05.

.

Розв’язок.

На основі побудованого графіка функції визначаємо відрізок, який містить корінь: [4.85; 5.2].

Крок 1

Крок 2

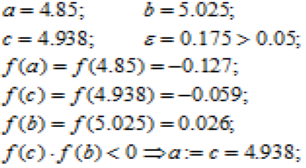
Крок 3

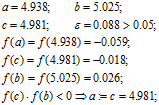
Крок 4

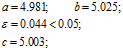
Таким чином, з заданною точністю знайдено корінь с = 5.003.

Приклад 3.3. Розглянемо застосування методу хорд для рівняння з прикладу 3.1.

.

На основі побудованого графіка функції був визначений відрізок, який містить корінь: [4.85; 5.2].

Таким чином

a = 4.85;     b = 5.2;

Знайдемо перше наближення до кореня:

Визначимо питому частину відрізку

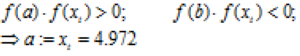
Запам’ятовується останнє наближення

Знайдемо наступне наближення:

.

Знову визначемо питому частину відрізку

Перевіряємо умову

Таким чином, знайдено наближений корінь x = 4.995. Аналізуючи кількість операцій, зазначимо, що розв’язок знайдено швидше, ніж методом половинного ділення.

Приклад 3.4.     Розглянемо приклад застосування методу Ньютона для задачі з прикладу 3.2.

.

На основі побудованого графіка функції був визначений відрізок, який містить корінь: [4.85; 5.2].

Таким чином

a = 4.85;     b = 5.2;

Визначимо початкове наближення:

Знайдемо наступні наближення до кореня:

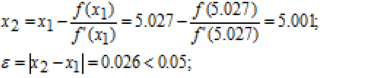
Таким чином, знайдено корінь х = 5.001

Приклад 3.5. Методом ітерацій знайти нуль функції з точністю 0,05.

Розв’язок.

Побудуємо графік функції.

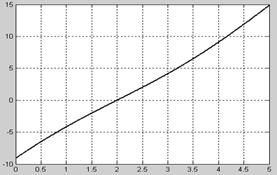
З графіка функції знаходимо відрізок, який містить корінь рівняння: [1.2; 2.2].

a = 1.2;     b = 2.2;

Представимо рівняння у вигляді:

Початкове наближення візьмемо як середину відрізка:

;

Знайдемо наступні наближення до кореня:

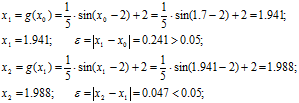
Таким чином, знайдено наближений нуль функції x = 1.988 з заданою точністю.

Приклад 3.6. Знайти корінь системи за допомогою метода Ньютона

Розв’язок.

Графічним шляхом можна знайти приблизно x₀ = 1,2 і y₀ = 1,7.

.

В початковій точці

= 97,910.

За формулами одержуємо

= 1,2 + 0,0349 = 1,2349;

= 1,7 – 0,0390 = 1,6610.

Продовжуючи процес обчислення при x₁ і y₁, отримаємо x₂ = 1,2343; y₂ = 1,6615 і т.д. до досягнення бажаної точності.

Приклад 3.7. Методом Ньютона наближено знайти додатний розв’язок системи

Розв’язок.

Позначимо . Вибравши за початкове наближення , отримаємо

.

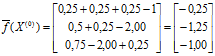     Побудуємо матрицю Якобі

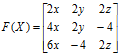, дістанемо .

Отримаємо систему рівнянь

.

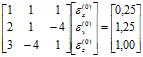Її розв’язок методом Гауса є

За знайденим приростом дістанемо перше наближення

.

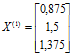Далі обчислюємо друге наближення Маємо

.

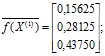
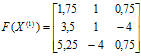Розв’язуючи систему рівнянь , отримуємо

; ;

Використовуючи знайдений приріст, будуємо друге наближення:

.

Аналогічно знаходимо третє наближення :

.

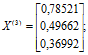
Його можна вважати шуканим розв’язком з точністю