
Чисельне рішення диференціальних рівнянь у пакеті MathCad
В MathCAD можна обчислювати похідні скалярних функцій будь-якої кількості аргументів, від 0- го до 5- го порядку включно. І функції, і
аргументи можуть бути як дійсними, так і комплексними.
Для того, щоб продиференціювати функцію f(х) у деякій точці потрібно:
панелі Calculus;
Наприклад,
|
|
|
|
Для рішення диференціальних рівнянь Mathcad надає користувачеві бібліотеку вбудованих функцій Dіfferentіal Equatіon Solvіng, призначених для чисельного рішення диференціальних рівнянь.
Вбудована функція odesolve призначена для рішення диференціальних рівнянь, лінійних щодо старшої похідної. Функція odesolve вирішує поставлене завдання методом Рунге- Кутта з фіксованим кроком. Звертання до функції має вигляд
Y:=odesolve(x,b,step) або Y:=odesolve(x,b),
де Y – ім'я функції, що містить значення знайденого рішення, x – змінна інтегрування, b – кінець проміжку інтегрування, step – крок, що використовується при інтегруванні рівняння методом Рунге- Кутта.
Приклад 14. Знайти за допомогою функції odesolve на відрізку ![]() рішення задачі Коші.
рішення задачі Коші.
![]()
![]()
![]()
![]()
![]()
У результаті змінній y привласнюються значення чисельного рішення задачі Коші на відрізку![]() .
.
В Mathcad вирішити задачу Коші для диференціальних рівнянь, а також для систем диференціальних рівнянь можна за допомогою таких функцій:
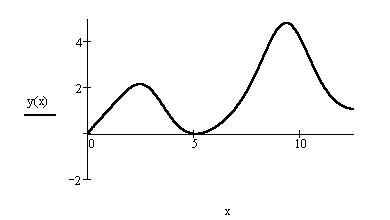
Приклад 15. Знайти на відрізку ![]() наближений розв’язок рівняння
наближений розв’язок рівняння ![]() , що задовольняє початковим умовам y(0)=1 і побудувати графік знайденого рішення.
, що задовольняє початковим умовам y(0)=1 і побудувати графік знайденого рішення.
Вирішимо завдання використовуючи алгоритм Рунге-Кутта з фіксованим кроком на сітці з 20 рівновіддалених вузлів.
Перш ніж вводити диференціальне рівняння, визначимо номер першого компонента вектора 1 (а не нулем, як передбачається за замовчуванням).
![]()
![]()
![]()
![]()
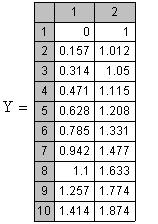
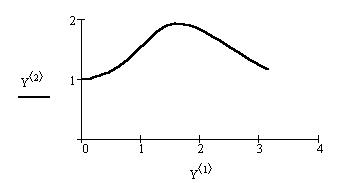
Приклад 16. Знайти на відрізку [0,3] наближене рішення задачі Коші
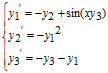
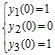
і побудувати графік знайденого рішення.
Вирішимо завдання використовуючи алгоритм Рунге-Кутта з фіксованим кроком на сітці з 20 рівновіддалених вузлів.
![]()
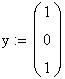
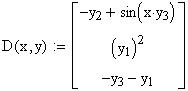
![]()
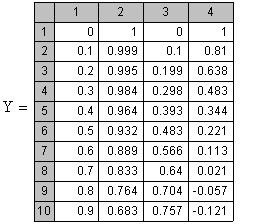
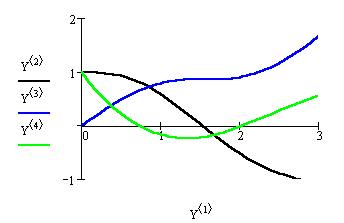
Приклад 17. Знайти розв’язок диференціального рівняння ![]() (
(![]() ).
).
Проаналізувавши результати, можна зробити висновок, що найвищу точність обчислень можна отримати за допомогою методу Рунге-Кутта
Рішення задач інтерполювання в середовищі MathCad
Пакет MathCad дозволяє виконувати інтерполяцію двох типів: кусково-лінійну і сплайнову. При лінійній інтерполяції MathCad з'єднує існуючі точки даних прямими лініями. Це виконується функцією linterp, яка повертає значення функції при її лінійному інтерполюванні.
linterp(vx, vy, x) використовує вектори даних ![]() і
і ![]() , щоб повернути значення, що інтерполюється
, щоб повернути значення, що інтерполюється ![]() , яке відповідає третьому аргументу
, яке відповідає третьому аргументу ![]() . Аргументи
. Аргументи ![]() й
й ![]() повинні бути векторами однакової довжини. Вектор
повинні бути векторами однакової довжини. Вектор ![]() повинен містити дійсні значення, розташовані в порядку зростання.
повинен містити дійсні значення, розташовані в порядку зростання.
Ця функція з'єднує точки даних відрізками прямих, створюючи таким чином ламану. Значення, що інтерполюється, для конкретного х є ордината у відповідної точки ламаної.
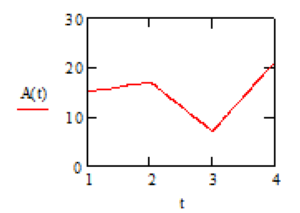
Приклад 18. Побудувати інтерполяційний многочлен Лагранжа третього ступеня для функції ![]() , заданої в таблиці та знайти наближене значення функції в точці
, заданої в таблиці та знайти наближене значення функції в точці ![]() .
.
x |
1 |
2 |
3 |
4 |
y |
15 |
17 |
7 |
21 |
![]()
![]()
![]()
Графічне відображення інтерполяційного многочлену Лагранжа.
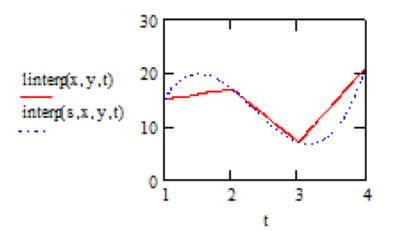
При невеликій кількості вузлових точок (менш ніж 10) лінійна інтерполяція є достатньо грубою. При її застосовуванні навіть перша похідна функції інтерполяції має різкі стрибки в вузлових точках.
В більшості практичних задач експериментальні дані бажано з’єднувати не ломаною лінією, а гладкою кривою, що дозволяє виконати сплайн-інтерполяція. При її застосуванні початкова функція замінюється відрізками кубічних поліномів, що проходить через три суміжні вузлові точки.
Порівняння результатів, отриманих в результаті застосовування лінійної інтерполяції і інтерполяції сплайнами:
Для здійснення сплайнової інтерполяції використовується функціяinterp(vs,vx,vy,x).
interp(vs,vx,vy,t) – функція, що апроксимує дані векторів ![]() и
и ![]() кубічними сплайнами, де vs - вектор других похідних, що створюється за допомогою однією з функцій cspline, pspline или lspline; vх – вектор дійсних даних аргументу, елементи якого розташовані в порядку зростання; vу - вектор дійсних даних того ж розміру; x – значення аргументу, при якому обчислюється функція.
кубічними сплайнами, де vs - вектор других похідних, що створюється за допомогою однією з функцій cspline, pspline или lspline; vх – вектор дійсних даних аргументу, елементи якого розташовані в порядку зростання; vу - вектор дійсних даних того ж розміру; x – значення аргументу, при якому обчислюється функція.
Іншими словами функція interp(vs,vx,vy,t) повертає значення ![]() , що інтерполюється, яке відповідає аргументу
, що інтерполюється, яке відповідає аргументу ![]() . Як вже зазначалося, вектор
. Як вже зазначалося, вектор ![]() обчислюється на основі векторів даних
обчислюється на основі векторів даних ![]() і
і ![]() однією з функцій pspline, lspline або cspline. Вони повертають вектор коефіцієнтів похідних 2-го порядку, що ми будемо називати vs. Аргументи vх й vу повинні бути дійсними векторами однакової довжини. Значення вектора vу повинні бути розташовані в порядку зростання.
однією з функцій pspline, lspline або cspline. Вони повертають вектор коефіцієнтів похідних 2-го порядку, що ми будемо називати vs. Аргументи vх й vу повинні бути дійсними векторами однакової довжини. Значення вектора vу повинні бути розташовані в порядку зростання.
Приклад 19. Використовуючи дані приклада 9 провести сплайн інтерполяцію.
![]()
Інтерполяція сплайнами з використанням функції lspline:
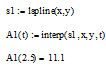
Інтерполяція сплайнами з використанням функції pspline:
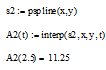
Інтерполяція сплайнами з використанням функції cspline:
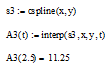
Результати інтерполяції заданих даних, отримані з використанням функцій lspline, pspline, cspline:
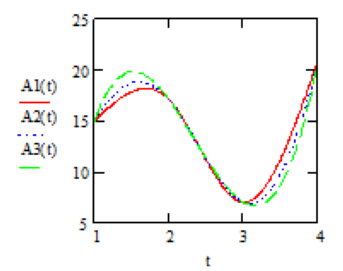
Запрограмуємо реалізацію методу Лагранжа. Формула Лагранжа в пакеті MathCad набуде наступного вигляду:
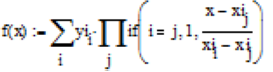 .
.
В результаті отримаємо:
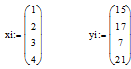
![]()
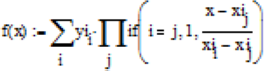
![]()
Результат інтерполяції, отриманий в результаті обчислень:
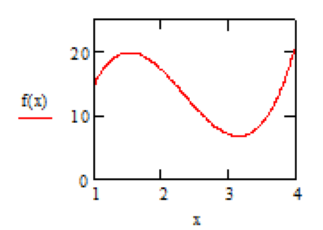
Приклад 20. Інтерполяція сплайнами:
Приклад 21. Апроксимація функції методом найменших квадратів