6.5 Рівноважний стан р-п переходу

Нехай внутрішньою межею поділу двох областей напівпровідника з різним типом провідності є площина ММ (рис. 6.9, а): зліва від неї знаходиться напівпровідник р-типу, наприклад, р-германий з концентрацією акцепторів , справа – напівпровідник n типу (n-германій) з концентрацією донорів . Для простоти вважатимемо, що і дорівнює, наприклад, 10²² м^-3. На рис. 6.9, б показана зміна концентрації акцепторних і донорних атомів при переміщенні уздовж осі х, перпендикулярної площини ММ. В точці 0, яка лежить в цій площині, N_a стрибкоподібно зменшується до нуля, а N_Д стрибкоподібно збільшується від нуля до N_Д.

Для n-області основними носіями є електрони, для р-області – дірки. Основні носії виникають внаслідок іонізації донорних і акцепторних домішок. При не дуже низьких температурах ці домішки іонізовані практично повністю, внаслідок чого концентрацію електронів в n-області n_n0 можна вважати рівною концентрації донорних атомів: n_n0= N_Д, а концентрацію дірок в р-області p_p0 – концентрації акцепторних атомів в р-області: p_p0 N_a.

Крім основних носіїв ці області містять неосновні носії: n-область – дірки (p_n0), р-область – електрони (n_p0). Їх концентрацію можна визначити, користуючись законом діючих мас: n_n0p_n0 = p_p0n_n0=n_i². При n_n0 = p_p0 = 10²²м^-3 і одержуємо .

Як бачимо, концентрація дірок в р-області на 6 порядків вища, ніж концентрація їх в n-області, так само концентрація електронів в n-області на 6 порядків вища їх концентрації в р-області. Така відмінність в концентрації однотипних носіїв в контактних областях напівпровідника приводить до виникнення дифузійних потоків електронів з n-області в р-область і дірок з р-області в n-область. При цьому електрони, що перейшли з n- в р-область, рекомбінують поблизу межі поділу цих областей з дірками р-області, так само дірки, що перейшли з р- в n-область, рекомбінують тут з електронами цієї області. В результаті цього в приконтактному шарі n-області практично не залишається вільних електронів і в ньому формується нерухомий об'ємний додатний заряд іонізованих донорів (рис. 6.9, а). В приконтактному шарі р-області практично не залишається дірок і в ньому формується нерухомий об'ємний негативний заряд іонізованих акцепторів. На рис. 6.9, в показано розподіл вільних носіїв заряду в області р-n-переходу, а на рис. 6.9,г – нерухомі об'ємні заряди, що утворилися в цьому переході (р – об'ємна густина цих зарядів). Позначимо товщину шару об'ємного заряду в р-області через d_р, в n-області через d_п, загальну товщину через d.

Нерухомі об'ємні заряди створюють в р-n-переході контактне електричне поле з різницею потенціалів V_k, локалізоване в області переходу і практично не виходить за його межі. Тому зовні цього шару, де поля немає, вільні носії заряду рухаються, як і раніше, хаотично і число носіїв, які щомиті натрапляють на шар об'ємного заряду, залежить тільки від їх концентрації і швидкості теплового руху.

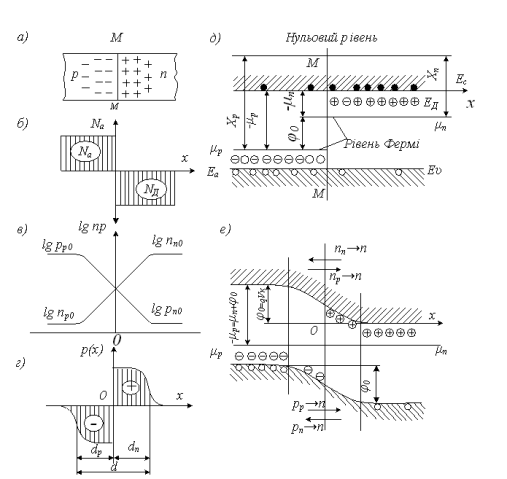
Рисунок 6.9 – Рівноважний стан р-n-переходу

Як випливає з кінетичної теорії газів, для частинок, що підлягають класичній статистиці Максвелла – Больцмана, це число п визначається таким співвідношенням:

          n = 1/4n₀(υ)S                                   (6.5)

де n₀ – концентрація частинок; υ – середня швидкість теплового руху; S – площа, на яку вони падають.

Неосновні носії – електрони з р-області і дірки з n-області, потрапляючи в шар об'ємного заряду (рис. 6.9, г), підхоплюються контактним полем і переносяться через р-n-перехід. Позначимо потік електронів, перехідних з р- в n-область, через n_p→n потік дірок, перехідних з n- в р-область, через p_n→p. Згідно з (6.5) маємо

n_p→n = n_{p0 n}S, (6.6)

p_n→p = p_{n0 p}S. (6.7)

Інші умови складаються для основних носіїв. При переході з однієї області напівпровідника в іншу вони повинні долати потенціальний бар'єр висотою що сформувався в р-n-переході. Для цього вони повинні мати кінетичну енергію руху уздовж осі х, не меншу . Згідно з (6.5) до р-n-переходу підходять такі потоки основних носіїв:

n⁰_p→n =n_{n0 n} S, p⁰_n→p =p_{p0 p} S.

Відповідно до закону Больцмана подолати потенціальний бар'єр зможе тільки n⁰_p→n∙exp(-qV_k /kT) електронів і p⁰_n→p exp(-qV_k /kT) дірок. Тому потоки основних носіїв, що проходять через р-n-перехід, рівні

n⁰_p→n =n_n0n exp(-qV_k /kT),                     (6.8)

p⁰_n→p =p_p0p exp(-qV_k /kT).                    (6.9)

На перших порах після уявного приведення n- і р-областей в контакт потоки основних носіїв значно перевершують потоки неосновних носіїв: n_n→p n_p→n, p_p→n p_n→p. Але у міру зростання об'ємного заряду збільшується потенціальний бар'єр р-n-переходу qV_k і потоки основних носіїв згідно з (6.8) і (6.9) різко зменшуються. В той же час потоки неосновних носіїв, не залежні від qV_k див. (6.6) і (6.7) залишаються незмінними. Тому відносно швидко потенціальний бар'єр досягає такої висоти j₀= qV_k, при якій потоки основних носіїв порівнюються з потоками неосновних носіїв:

               n_n→p =n_p→n ,                         (6.10)

               p_p→n = p_n→p .                              (6.11)

Це відповідає встановленню в р-n-переході стану динамічної рівноваги.

Підставляючи в (6.10) з (6.8) і з (6.6), а в (6.11) з (6.9) і з (6.7), одержуємо

               n_n0 exp (-qV_k/kT) = n_p0,                    (6.12)

               p_p0 exp (-qV_k/kT) = p_n0.                    (6.13)

Звідси легко визначити рівноважний потенціальний бар'єр р-n-переходу = qV_k. Із (6.12) знаходимо

φ₀ = qV_k = kT ln(n_n0 /n_p0) = kT ln(p_p0n_n0 /n_i²).     (6.14)

З (6.13) одержуємо

φ₀ = kT ln(p_p0 /p_n0) = kT ln(p_p0n_n0 /n_i²).          (6.15)

З (6.14) і (6.15) витікає, що вирівнювання зустрічних потоків електронів і дірок відбувається при одній і тій же висоті потенціального бар'єра . Цей бар'єр тим вищий, чим більша відмінність в концентрації носіїв одного знака в n- і р-областях напівпровідника. На рис. 6.9,д показана зонна діаграма р- і n-областей напівпровідника у момент уявного їх зіткнення, тобто до встановлення між ними рівноваги. Енергетичні рівні зображаються горизонтальними прямими. Це показує той факт, що енергія електрона, що знаходиться на даному рівні, наприклад, на дні зони провідності, в усіх точках напівпровідника однакова. Після встановлення рівноваги утворюється р-n-перехід з потенціальним бар'єром для основних носіїв, рівним φ₀=qj₀V_k. Електрони, перехідні з n- в р-область, долаючи цей бар'єр збільшують свою потенціальну енергію на φ₀=qV_k. Tому всі енергетичні рівні напівпровідника, скривлюючись в області р-n-переходу, підіймаються вгору на φ₀, як показано на рис. 6.9, е. При цьому рівні Фермі μ_n і μ_p встановлюються на одній висоті, як і у разі контакту двох металів (рис. 6.7, б).