|
1.1.2 Оптичні системи для зменшення розходження променів лазера
Збільшення просторової щільності потоку випромінювання лазера при передаванні його енергії на великі відстані обумовлює необхідність зменшення кута розходження. “Ідеальний” лазер, що має плоский хвильовий фронт, генерує пучок променів, кут розходження якого визначається дифракцією
2wД = 1,22l¤d, (1.13)
де d – діаметр вихідного торця лазера. Застосовувані на практиці лазери мають кути розходження, більше
2wД, і для різних типів лазерів ці кути складають від декількох хвилин до декількох градусів. Для зменшення кута розходження лазерних пучків використовуються двокомпонентні лінзові (рис. 2.3) чи дзеркальні насадки, що складаються з першої негативної і другої позитивної компонент (обернена телескопічна система).
 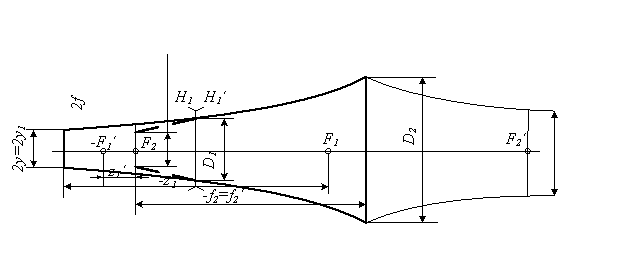
Рисунок 1.3 – Двокомпонентна система для зменшення розходження лазерного пучка
Основними характеристиками афокальної насадки для лазера є кутове збільшення g, кутове поле
2w¢, діаметр вхідної зіниці D, положення вхідної зіниці
aR щодо першого компонента, довжина насадки L, довжина хвилі l випромінювання лазера.
Кутове збільшення (розраховують з урахуванням виразів (1.6), (1.12) – (1.14) за формулою
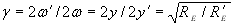 , (1.15) , (1.15)
де 2у = 2у¢ і
2у¢ = 2у2¢, RE = RE1 і
RE¢ = RE2¢ – діаметри перетяжок і конфокальні параметри лазерного і перетвореного пучків променів [3].
Кутове поле 2w¢ визначається кутом розходження пучків променів у просторі зображень. Діаметр вхідної зіниці D дорівнює діаметру вихідного торця лазера d і діаметру 2у перетяжки лазера. Положення ар вхідної зіниці визначається відрізком а1 від перетяжки лазера до першої компоненти. Довжина насадки
L=f¢1+f¢2,
де f¢1,
f¢2
– задні фокусні відстані компонентів насадки.
Для забезпечення мінімального розходження пучка після оптичної системи необхідно з’єднати перетяжку пучка, перетвореного першою компонентою, з передньою фокальною площиною другої компоненти. Відстань (оптичний інтервал), що визначає зсув заднього фокуса першої компоненти відносно переднього фокуса другої компоненти згідно з (1.10)
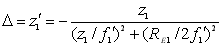 . (1.16) . (1.16)
Кутове збільшення
 розфокусованої системи розфокусованої системи
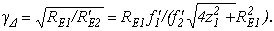 (1.17) (1.17)
При D = 0 кутове збільшення афокальної насадки визначається залежністю
g = -f¢1/f¢2. (1.18)
З аналізу формул (1.15), (1.17), (1.18) видно, що кут розходження пучка після розфокусованої системи менший, ніж після афокальної насадки.
Таким чином, при розрахунку розглянутої двокомпонентної системи для зменшення розходження пучка лазера на підставі формул, отриманих з дифракційної теорії, визначають такі величини (за умови, що тип лазера, l, RE, 2y, 2w – відомі):
- кутове збільшення g насадки за формулою (1.15);
- діаметр D1 першої компоненти за формулою (1.5), де x = 2a1/RE; a1 – положення перетяжки лазера відносно головних площин першої компоненти (вибирається з конструктивних міркувань);
- фокусна відстань першої компоненти
f¢1 (відношення
D1/f¢1 обирають не вище ніж 1/5);
- D – оптичний інтервал знаходять за формулою (1.16), де
z1=a1+fў1; RE1=RE;
- конфокальний параметр R¢E1 пучка, перетвореного першою компонентою, за формулою
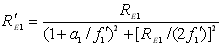 ; (1.19) ; (1.19)
- діаметр
2y1¢ перетяжки пучка, перетвореного першою компонентою
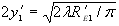 ; (1.20) ; (1.20)
- фокусна відстань другої компоненти з (1.17)
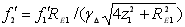 ; (1.21) ; (1.21)
- діаметр D2, другої компоненти
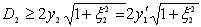 , (1.22) , (1.22)
де x2 = 2а2/RE2
= -2f¢2/RўE1.
Розрахунок насадки на основі законів геометричної оптики аналогічний розрахунку телескопічної системи для конкретного лазера (l, D,
2w – відомі).
Нижче наведені розрахункові формули
g = 2w¢/2w; D¢ = D/g; D1 = D+2aRw; D2 = D¢, (1.23)
f¢1 = D1K;
f¢2
= -f¢1/g;
L = f¢1+f¢2, (1.24)
де K – діафрагмове число, яке не має бути більше 3 (іноді 2).
В даному параграфі було розглянуто перетворення лазерних пучків тільки в гаусовому наближенні. Оптична система вважається ідеальною, якщо світловий пучок, що входить в неї, знову перетворюється в чисто гаусовий пучок. Це можливо тільки за умови, що оптична система не вносить додаткових спотворень у форму хвильового фронту. При розрахунку оптичних систем, коли необхідно знати точну структуру лазерного пучка, сформованого системою, може бути рекомендований метод скалярної теорії дифракції [8].
Розбіжність світлового пучка у просторі характеризується тілесним кутом, в межах якого поширюється основна частина випромінювання. Нелазерні джерела світла мають малу направленість випромінювання (в межах тілесного кута від
2p до 4p), інтенсивність якого змінюється відповідно до закону Ламберта. На великій відстані від джерела сферична хвиля наближається до плоскої, якій властива так звана дифракційна розбіжність (формула 1.13). Однак розбіжність лазерного випромінювання пов`язана не тільки з дифракцією плоских хвиль на вихідній апертурі лазера, але і з геометрією оптичного резонатора. Тому поруч з дифракційною відрізняють також геометричну розбіжність лазерного випромінювання, що характеризується кутом wгеом .
Повний кут розбіжності для моди ТЕМmn (m, n Ј 5) дорівнює
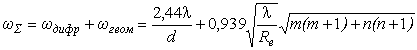 . (1.25) . (1.25)
При цьому
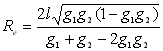 , ,
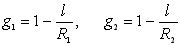 – параметри конфокальності резонатора, R1 та R2 – радіуси лазерних дзеркал. – параметри конфокальності резонатора, R1 та R2 – радіуси лазерних дзеркал.
При вимірюванні розбіжності лазерного променя необхідно враховувати структуру поля у ближній та дальній зонах. Дифракція на вихідній апертурі, розсіювання на неоднорідностях активного середовища призводять до створення сильно розбіжної компоненти випромінювання, яка зменшується практично до нуля на відстані
z0 = d2/l (z – напрямок розповсюдження випромінювання). При z > z0 розповсюджується компонента випромінювання з практично плоским фронтом, яка добре описується наближенням Фраунгофера. Таким чином, при z < z0 формується ближня зона лазерного променя (область Френеля), а при z > z0 – дальня зона (область Фраунгофера). Розбіжність лазерного променя визначають у дальній зоні, хоча це й не завжди можливо у лабораторних умовах (наприклад, для d = 2 мм та l = 0,44 мкм величина
z0 » 9 м).
1.2 Завдання та хід виконання роботи
1. Вивчити теоретичні питання, пов’язані з керуванням лазерним випромінюванням у адаптивних оптичних системах.
2. Зібрати на оптичному столі (лаві) схему для дослідження розходження лазерного випромінювання у дальній зоні (область Фраунгофера).
3. Для газового He-Ne лазера ЛГ-602Н (l = 0,6328
мкм) виміряти необхідні величини (довжина резонатора, діаметр світлової апертури d, експериментальний кут
wS
розходження променя).
4. Визначити за формулою 1.13 дифракційну розбіжність випромінювання газового лазера wдифр.
5. У наближенні концентричного оптичного резонатора для основних мод (0,1 та 1,1) даного лазера розрахувати:
- параметри конфокальності та радіуси кривизни поверхонь лазерних дзеркал;
- положення та діаметр перетяжки, конфокальний параметр лазерного резонатора за формулами (1.1) – (1.4).
6. Встановити на відстані 20 см від лазерного випромінювача тонку збиральну лінзу із великою фокусною відстанню (f > 50cм).
7. Розрахувати для перетвореного даною лінзою лазерного пучка:
- конфокальний параметр
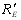 перетвореного пучка за формулою (1.11) за заданим діаметром 2у' перетяжки; перетвореного пучка за формулою (1.11) за заданим діаметром 2у' перетяжки;
- фокусну відстань fў оптичної системи з виразів (1.7) – (1.8) (відстані а та z вибрати за конструктивними міркуваннями);
- діаметр вхідної зіниці D (DT.C. = D) за формулою (1.5) за умови
D і 2ys;
- положення а' та zў перетяжки пучка за формулами (1.9) і (1.10).
8. Встановити між лазером та лінзою афокальну насадку для зменшення розбіжності променя (рис. 1.3).
9. Визначити кутове збільшення g та
кутове поле
2wў
встановленої насадки, а також еквівалентну фокусну відстань трикомпонентної
оптичної системи (лінза + насадка).
10. Розрахувати параметри афокальної насадки, яка забезпечить зменшення розбіжності променя заданого лазера у 50 разів (за формулами 1.5-1.18).
11. Побудувати графічні залежності
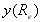 , ,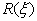 , ,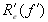 , ,
 . .
12. Cкласти звіт.
Контрольні запитання
1. Оптичні резонатори лазерів.
2. Характеристики оптичних резонаторів
3. Параметри конфокальності оптичних резонаторів. Умова стійкості.
4. Положення та діаметр перетяжки лазерного пучка.
5. Радіус хвильового фронту променя.
6. Радіус еквівалентності.
7. Перетворення лазерного пучка тонкою лінзою.
8. Оптичні системи для зменшення розбіжності світлових пучків.
9. Основні параметри афокальної насадки.
|