4.2.1 Критерії оцінювання нерівномірності групового графіка навантажень

Груповий графік навантажень формується шляхом накладання індивідуальних графіків, хід яких обумовлюється технологічним про-цесом:

де P(t) – груповий графік навантаження;

pi(t) – індивідуальний графік навантаження для i-го електроприймача;

m – загальна кількість електроприймачів, які формують груповий графік навантаження.

В термінах теорії ймовірності графіки навантаження є випадковими процесами. Подамо випадкові процеси P(t) та p_i(t) як послідовності випадкових величин P та pi. Для задачі, що розглядається, визначимо такі параметри розподілу зазначених величин, як середні їх значення (математичні сподівання M(P) та M(pi)) та кількісні характеристики їх розкиду відносно середнього значення (дисперсії D(P) та D(pi)).

Математичне сподівання для випадкової величини pi визначається так:

де n – загальна кількість спостережень величини pi.

Математичне сподівання для величини P можна виразити через мате-матичні сподівання її складових:

Нерівномірність графіка навантаження прийнято оцінювати коефіцієнтом форми графіка, але ще одним із показників його нерівномірності може бути дисперсія. Маючи необхідний статистичний матеріал, дисперсію випадкової величини pi можна розрахувати таким чином:

Значення дисперсії величини P через відповідні параметри системи випадкових величин pi запишеться так:

Вплинути на значення дисперсії D_(pi) можливо тільки змінивши хід індивідуального графіка, що практично можна здійснити лише змінивши технологічний процес. Тому згідно з умовою задачі D_(pi) будемо вважати сталою величиною. Для того, щоб зробити висновки щодо другої складової, розглянемо приклад.

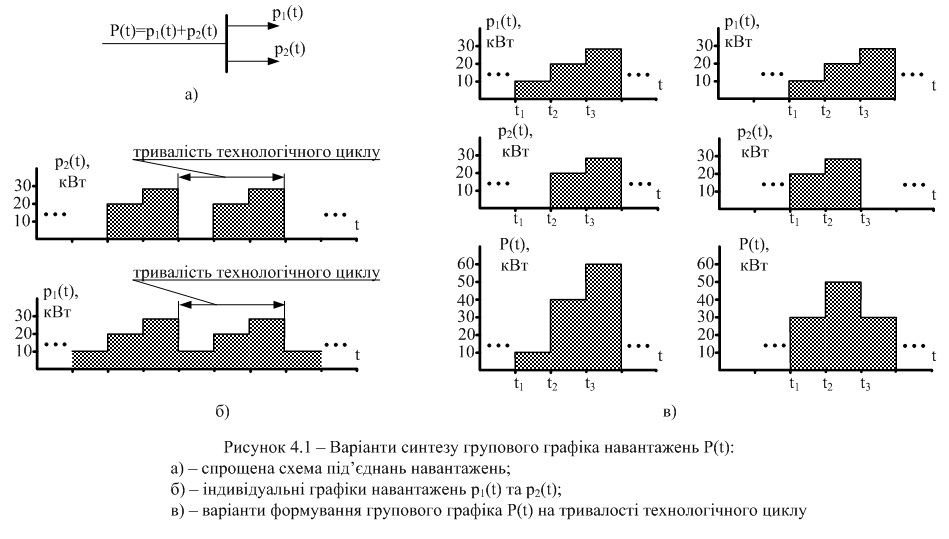
ПРИКЛАД 4.1. Груповий графік навантаження формується двома електроприймачами, які під’єднані до мережі за схемою, рис. 4.1, а та мають індивідуальні графіки та , рис. 4.2, б. Графіки та можуть мати варіанти зсуву в часі, рис. 4.1, в.

Значення p₁(t) та p₂(t) для ряду перерізів часу ti наведені в табл. 4.1 для двох варіантів.

Зробити обчислення D(P) для групових графіків навантаження, які формуються у випадку варіантів 1 та 2.

РОЗВ’ЯЗАННЯ. 1. Дисперсії випадкових величин p1 та p2 –

D(p1) = 66,6 кВт²; D(p2) = 155,55 кВт².

2. Кореляційні моменти відповідно для варіантів 1 та 2 –

3. Дисперсії групових графіків навантаження, що отримуються в 1 та 2 варіантах –

D(P) =66,6 + 155,55 - 2×11,06 = 200 кВт²;

D(P) =66,6 + 155,55 - 2×66,66 = 88,83 кВт².

З результатів, одержаних в прикладі 4.1, видно, що отримані значення дисперсії, а, отже, і нерівномірність отриманих групових графіків за варіантами 1 та 2 – різні. Відмінність результатів пояснюється різними значеннями кореляційних моментів випадкових величин потужностей p¹ та p², які залежать від відносного зсуву в часі між індивідуальними графіками навантаження. Такий висновок можна поширити на будь-яку кількість індивідуальних графіків. Таким чином, задача синтезу групового графіка навантаження є оптимізаційною, оскільки, змінюючи відносний зсув в часі між індивідуальними графіками, можна варіювати нерівномірність групового. Критерієм для пошуку оптимального зсуву між графіками є сума для якої необхідно забезпечити мінімальне значення.