Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
1.7.3 Переведення правильних дробів з однієї позиційної системи числення в іншу
Нехай задана дробова частина 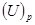 числа
числа 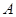 (правильний дріб) у довільній позиційній системі числення з основою р:
(правильний дріб) у довільній позиційній системі числення з основою р:
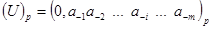
і її необхідно перевести в нову систему числення з основою r, тобто звести до такого вигляду:
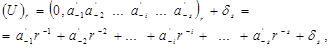
де 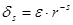 – похибка округлення (
– похибка округлення (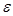 < 1).
< 1).
Цифри 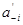 представляють собою цілу частину, яка утворюється при множенні на нову основу
представляють собою цілу частину, яка утворюється при множенні на нову основу 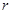 , задану в позиційній системі числення з основою р, дробової частини
, задану в позиційній системі числення з основою р, дробової частини 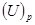 числа
числа 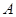 і наступних дробових частин
і наступних дробових частин 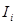 аж до отримання заданої кількості цифр із врахуванням необхідної точності згідно з наступною схемою:
аж до отримання заданої кількості цифр із врахуванням необхідної точності згідно з наступною схемою:
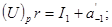
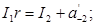
...
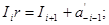
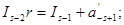
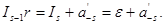
Доведення правильності такого алгоритму теж очевидне. Із (1.18) отримаємо:
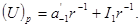
З урахуванням того, що
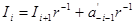
для 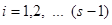 можна отримати
можна отримати
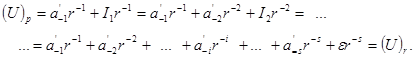
Тобто цілі частини від множення згідно з алгоритмом (1.18) є цифрами представлення дробової частини 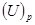 числа
числа 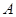 у позиційній системі числення з основою
у позиційній системі числення з основою 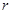 , що і необхідно було довести.
, що і необхідно було довести.
Правило переведення правильних дробів із однієї позиційної системи числення в іншу формулюється таким чином: щоб перевести правильний дріб із однієї позиційної системи числення в іншу, необхідно початкове число послідовно множити на основу нової системи числення, записану в початковій системі числення. Число у новій системі числення записується із цілих частин від множення, починаючи із першої. Процедуру необхідно продовжувати до отримання заданої точності.
Як видно з останнього виразу, на відміну від цілих чисел, точне переведення можливе не для всіх правильних дробів. Похибка при переведенні визначається одиницею молодшого розряду запису числа в системі числення з основою 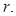
Приклад. Перевести правильний дріб 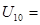 0,357 із десяткової системи числення у двійкову, вісімкову і шістнадцяткову системи числення.
0,357 із десяткової системи числення у двійкову, вісімкову і шістнадцяткову системи числення.
Процедура переведення згідно із розглянутим алгоритмом представлена у табл. 1.8.
|
|
|
|
|||
|
Ціла частина |
Дробова частина |
Ціла частина |
Дробова частина |
Ціла частина |
Дробова частина |
|
0
0
1
0
1
1
0
1
1
0
1 |
357
714
428
856
712
424
848
696
392
78
568 |
0
2
6
6
6 |
357
856
848
784
272 |
0
5
4
4
|
357
712
272
352
|
Із врахуванням результатів табл. 1.8, отримаємо:
0,35710 = 0,01011011012 = 0,26668 = 0,54416.
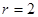
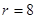
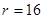
 2
2