Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
1.7.2 Переведення цілих чисел з однієї позиційної системи числення в іншу
Нехай задана ціла частина 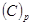 числа
числа  в довільній позиційній системі числення з основою р:
в довільній позиційній системі числення з основою р:
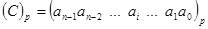 ,
,
і його необхідно перевести в нову систему числення з основою r, тобто звести до такого вигляду:
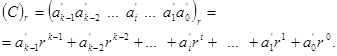
Цифри 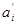 представляють собою остачу від ділення на нову основу
представляють собою остачу від ділення на нову основу 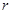 , задану в позиційній системі числення з основою р, цілої частини
, задану в позиційній системі числення з основою р, цілої частини 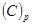 числа
числа 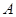 і наступних цілих частин частки
і наступних цілих частин частки 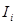 аж до отримання цілої частини від ділення
аж до отримання цілої частини від ділення 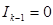 згідно з такою схемою:
згідно з такою схемою:
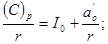
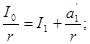
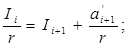
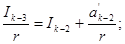
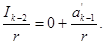
Доведення такого алгоритму очевидне. Із (1.16) можна записати:
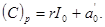
Із врахуванням того, що
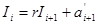
для 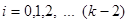 , можна отримати:
, можна отримати:
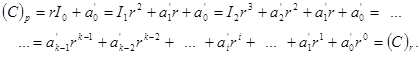
Тобто остачі від ділення згідно з алгоритмом (1.16) є цифрами представлення цілої частини 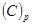 числа
числа 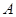 у позиційній системі числення з основою
у позиційній системі числення з основою 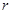 , що і необхідно було довести.
, що і необхідно було довести.
Правило переведення цілих чисел із однієї позиційної системи числення в іншу формулюється таким чином: щоб перевести ціле число з однієї позиційної системи числення в іншу, необхідно початковечисло послідовно ділити на основу нової системи числення, записану в початковій системі числення, до отримання частки, яка дорівнює нулю. Число у новій системі числення записується із остач від ділення, починаючи з останньої.
Приклад. Перевести десяткове число С10 = 345 у двійкову, вісімкову і шістнадцяткову системи числення.
Виконаємо дії згідно з наведеним вище алгоритмом і отримаємо:
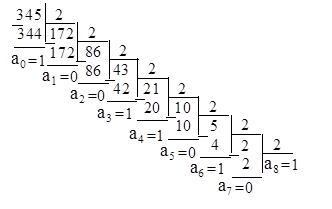
Тобто 34510 = 1010110012.
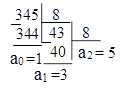
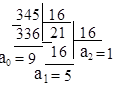
34510 = 5318