Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.7.5. Переведення чисел із систем числення з кратними основами

В цифровій техніці широке застосування знаходять вісімкова і шістнадцятькова системи числення, основи яких є степенями числа 2 (основи двійкової системи числення).

Якщо основи систем числення кратні один одному, тобто пов’язані залежністю

 

(1.19)

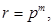
то кожна цифра системи числення з основою 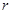  може бути зображена  m цифрами в системі числення з основою р (хоча загальні правила переведення чисел із однієї позиційної системи числення в іншу за допомогою послідовного ділення і множення залишаються в силі і в цьому випадку).

Доведення розглянемо на прикладі переведення числа 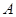 із вісімкової системи числення у двійкову.

Згідно з (1.5) можна записати:

 

(1.20)

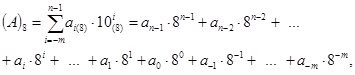
де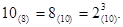 

Будь-яка вісімкова цифра може бути представлена у вигляді трирозрядного двійкового числа, тобто у вигляді тріади двійкових цифр:

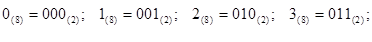
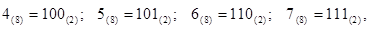
або в загальному випадку у вигляді такої суми

 

(1.21)

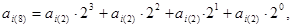
де 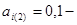ображення будь-якої двійкової цифри.

Підставимо значення (1.20) у формулу (1.19):

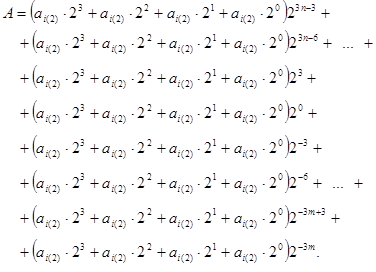
Розкриємо дужки і отримаємо:

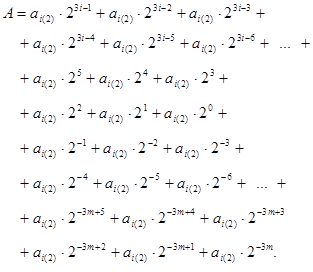
Виконавши процедуру згортання останнього виразу, отримаємо:

 

(1.22)

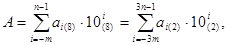
що і необхідно було довести.

Виконавши аналогічні перетворення при переведенні із шістнадцятькової системи числення у двійкову, можна отримати:

 

(1.23)

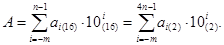
Отже, для того щоб перевести число з початкової системи числення в нову систему, основа якої кратна основі початкової системи, досить кожну цифру числа, що переводиться, записати за допомогою m  цифр у новій системі числення, якщо основа початкової системи числення більша від основи нової системи числення. У іншому разі кожні m  цифр початкового числа необхідно записати за допомогою однієїцифри в новій системі числення, починаючи для цілих чисел з молодшого розряду і зі старшого розряду для правильних дробів.

Наприклад,  при  переведенні  вісімкового  числа 316₈  у двійкову систему числення досить кожну цифру вісімкового числа записати у вигляді двійкової тріади, оскільки 8 = 2³:

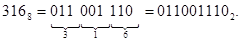
При переведенні, наприклад, двійкового числа в шіснадцаткову систему числення досить кожну тетраду початкового числа записати у вигляді шістнадцяткової цифри: