Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
2.3 Доповнення в позиційних системах числення
В позиційних системах числення з основою р для 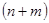 - розрядного числа
- розрядного числа
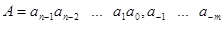
вводиться два визначення доповнення:
• доповнення до р
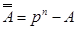 для
для 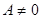 ,
,
(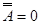 для
для 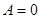 )
)
• доповнення до (р - 1)
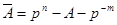
В залежності від значення основи системи числення застосовуються такі назви доповнень:
- доповнення до двох (двійкове) і доповнення до одиниці (одиничне) (р = 2);
- доповнення до восьми (вісімкове) і доповнення до семи (сімкове) (р = 8);
- доповнення до десяти (десяткове) і доповнення до дев’яти (дев’яткове) (р = 10);
- доповнення до шістнадцяти (шістнадцяткове) і доповнення до п’ятнадцяти (п’ятнадцяткове) (р = 16).
Варто зазначити, що двократне доповнення заданого числа є самим числом, тому що:
- доповнення до р доповнення до р числа А визначається так
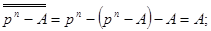
- доповнення до (р - 1) доповнення до (р - 1) числа А визначається так:
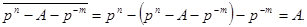
Необхідно відмітити, що доповнення до р можна обчислити, як суму доповнення до (р - 1) і одинички молодшого розряду 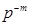
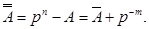
Приклад.
а) для десяткового числа А = 1636,67110 маємо
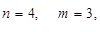
- доповнення десяткове 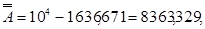
- доповнення дев’яткове 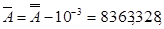
б) для двійкового числа А = 110,10 маємо:
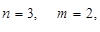
- двійкове доповнення 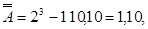
- одиничне доповнення 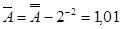 .
.
З наведених визначень і розглянутого прикладу випливає, що для числа А, заданого в позиційній системі числення з основою р, будуть справедливі такі співвідношення:
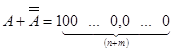
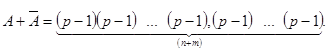
Як легко зауважити, доповнення до (р - 1) для числа, заданого в позиційній системі числення з основою р, найпростіше обчислити за допомогою віднімання кожної цифри числа від (р - 1). Тобто
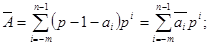
де 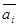 - доповнення до (р - 1) цифри
- доповнення до (р - 1) цифри 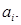
Тоді, з урахуванням (2.17), отримаємо
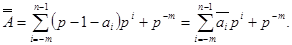
Алгоритм такого перетворення розглянемо на наступних прикладах.
Приклад.



У випадку використання кодування десяткових чисел двійковими кодами, що самодоповнюються, досить легко обчислити дев’яткове доповнення десяткових цифр. Це доповнення отримується через одиничне доповнення кожного біту коду (заміна 0 на 1 і 1 на 0 у кожному біті).
Приклад. Виконаємо вказану процедуру для числа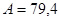 , заданого в коді 8421 плюс 3:
, заданого в коді 8421 плюс 3:
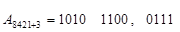
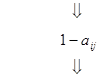
- доповнення дев’яткове 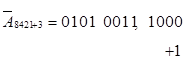
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
- доповненнядесяткове 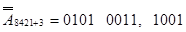
Якщо для кодування використовується код 8421, який не має властивості самодоповнення, розглянутий вище спосіб необхідно модифікувати за допомогою введення корекції, яка полягає у додаванні до кожної тетради коректуючого коду 0110.
Приклад. Десяткове число А = 79,4 в коді 8421 має такий вигляд:
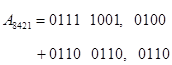
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
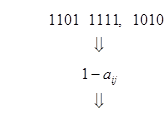
- доповнення дев’яткове 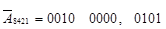

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
- доповнення десяткове 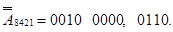
Використання розглянутих понять доповнень дозволяє спростити виконання операцій віднімання в позиційних системах числення з основою р.