Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
2.2 Загальні правила виконання арифметичних операцій в системах числення з основою р
Як показано в першій главі, позиційні системи числення мають чіткі і певні міжрозрядні зв’язки. Цю їх властивість можна розглядати як перевагу, оскільки вона забезпечує простоту виконання арифметичних операцій, але, разом з тим, і як недолік, оскільки ця властивість через наявність міжрозрядних перенесень призводить до обмеження технічної швидкості виконання арифметичних операцій.
Арифметичні операції додавання, віднімання і множення двох 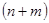 розрядних чисел
розрядних чисел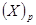 і
і 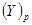
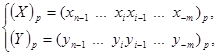
в системі числення з основою р можна розглядати, як виконання вказаних операцій над окремими розрядами заданих чисел.
Результатом виконання операцій над цифрами і-го розряду 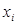 і
і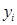 в системі числення з основою р є дві цифри:
в системі числення з основою р є дві цифри:
• 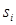 - результат операції у і-му розряді;
- результат операції у і-му розряді;
• 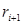 - перенесення в наступний (і+1)-й розряд (для додавання і множення).
- перенесення в наступний (і+1)-й розряд (для додавання і множення).
При виконанні основних арифметичних операцій можна сформулювати такі алгоритми формування цифр 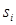 і
і 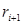 :
:
• додавання
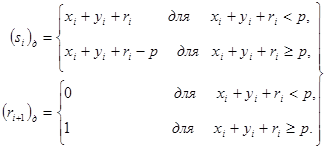
• віднімання
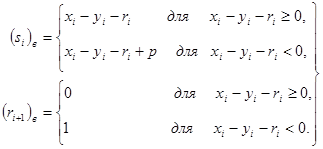
• множення
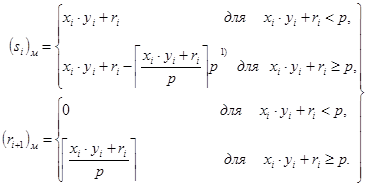
У двійковій системі числення операція множення значно спрощується у зв’язку з тим, що завжди перенесення 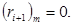
Для обчислення 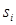 і
і 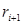 при виконанні решта операцій у двійковій системі числення можна скористатись табл. 2.1.
при виконанні решта операцій у двійковій системі числення можна скористатись табл. 2.1.
|
x |
y |
|
|
|
||
|
|
|
|
|
|
||
|
0 0 1 1 |
0 0 1 1 |
0 1 1 0 |
0 0 0 1 |
0 1 1 0 |
0 1 0 0 |
0 0 0 1 |
Реалізація операції ділення двох чисел не може бути виконана над однорозрядними цифрами.
У випадку виконання операцій над двійково-десятковими цифрами необхідно взяти до уваги результат, який виникає з урахуванням особливостей кодування.
Розглянемо виконання операції додавання двох двійко-во-десяткових цифр 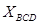 і
і 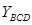
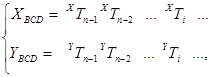
а також можливі варіанти перенесення 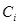 з
з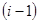 -ої тетради.
-ої тетради.
У випадку додавання
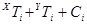
можна отримати результат, який дорівнює 0,1, ... ,18 або 19.
В табл. 2.2 - 2.4 наведені результати додавання еквівалентів двійкових цифр 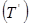 , а також їх дійсна сума
, а також їх дійсна сума 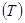 для кодів:
для кодів:
1. 8421 (таблиця 2.2);
2. 8421 + 3 (таблиця 2.3);
3. 2421 (таблиця 2.4).
Алгоритми додавання для вказаних кодів можна сформулювати наступним чином:
1. Код 8421
- для 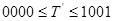 , маємо
, маємо 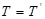 (корекція не потрібна);
(корекція не потрібна);
- для 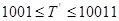 , маємо
, маємо 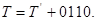
2. Код 8421+3
- для 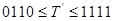 , маємо
, маємо 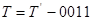 або
або 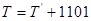 (при цьому перенесення, що виникає у тетраді, належить опускати);
(при цьому перенесення, що виникає у тетраді, належить опускати);
- для 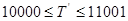 , маємо
, маємо 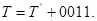
У цьому випадку значення необхідної корекції залежить від перенесення 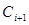 :
:
- якщо 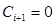 , то
, то 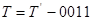 або
або 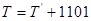 (перенесення з тетради опускається);
(перенесення з тетради опускається);
- якщо 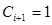 , то
, то 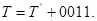
3. Код 2421
- для 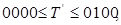
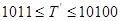 (при
(при 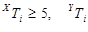 < 5),
< 5), 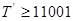 , маємо
, маємо 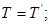
- для 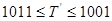 (при
(при 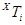 < 5,
< 5, 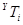 < 5), маємо
< 5), маємо 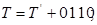
- для 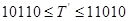 (при
(при 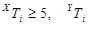
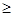 5), маємо
5), маємо 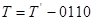 або
або 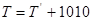 (перенесення з тетради необхідно опускати).
(перенесення з тетради необхідно опускати).
|
Сума десяткова |
|
Примітки |
|
|
|
|
||
|
0 1 2 3 4 5 6 7 8 9 |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 |
|
|
10 11 12 13 14 15 16 17 18 19 |
1010 1011 1100 1101 1110 1111 1 0000 1 0001 1 0010 1 0011 |
1 ← 0000 1 ← 0001 1 ← 0010 1 ← 0011 1 ← 0100 1 ← 0101 1 ← 0110 1 ← 0111 1 ← 1000 1 ← 1001 |
|
|
Сума десяткова |
|
Примітки |
|
|
|
|
||
|
0 1 2 3 4 5 6 7 8 9 |
0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 |
або
(при цьому перенесення, що виникає із тетради, не враховується |
|
10 11 12 13 14 15 16 17 18 19 |
1 0000 1 0001 1 0010 1 0011 1 0100 1 0101 1 0110 1 0111 1 1000 1 1001 |
1 ← 0011 1 ← 0010 1 ← 0101 1 ← 0110 1 ← 0111 1 ← 1000 1 ← 1001 1 ← 1010 1 ← 1011 1 ← 1100 |
|
|
Сума десяткова |
|
Примітки |
|||
|
|
|
||||
|
0 1 2 3 4 |
0000 0001 0010 0011 0100 |
0000 0001 0010 0011 0100
|
|
||
|
|
|
|
|
|
|
|
5 6 7 8 9 |
1011 1100 1101 1110 1111
|
1011 0110 0111 1000 1001 |
1011 1100 1101 1110 1111 |
||
|
|
або
|
||||
|
10 11 12 13 14 |
1 0000 1 0001 1 0010 1 0011 1 0100 |
1 0110 1 0111 1 1000 1 1001 1 1010 |
1←0000 1←0001 1←0010 1←0011 1←0100
|
||
|
15 16 17 18 19 |
1 1011 1 1100 1 1101 1 1110 1 1111 |
1←1011 1←1100 1←1101 1←1110 1←1111 |
|
||
З аналізу таблиць видно, що:
1. правила додавання залежать від типу коду, що застосовується,
2. в деяких випадках необхідно провести корекцію результату.
Приклад. Виконати операції додавання
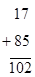
з використанням розглянутих BCD кодів.
а) код 8421
0000 0001 0111 (17)
+ 0000 1000 0101 (85)
————————
0000 1001 1100
+ 0110 (корекція 1)
————————
0000 1010← 0010
+ 0110 (корекція 2)
————————
0001 0000 0010 (102)
б) код 8421 + 3
0011 0100 1010 (17)
+ 0011 1011 1000 (85)
————————
0111 ← 0000 ← 0010
+ 1101 0011 0011 (корекція)
————————
(не враховується) ← 0100 0011 0101 (102)
в) код 2421
0000 0001 1101 (17)
+ 0000 1110 1011 (85)
————————
0001← 0000 ←1000
+ 1010 (корекція)
————————
0001 0000 ↓ 0010 (102)
(не враховується)
Тобто виявляється, що введення поправки (корекції) є багатогранним процесом і не можна у цьому випадку поставити в залежність введення поправки від наявності перенесення.
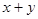
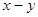
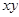
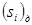
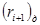
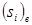
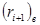
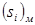
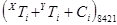
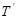
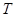
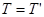
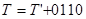
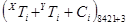
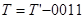
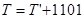
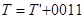
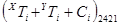
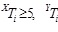 < 5
< 5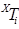 <5,
<5,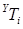 < 5
< 5