Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
2 ПРАВИЛА ВИКОНАННЯ АРИФМЕТИЧНИХ ОПЕРАЦІЙ В ПОЗИЦІЙНИХ СИСТЕМАХ ЧИСЛЕННЯ
2.1 Вибір основи системи числення для застосування в цифрових пристроях
Очевидно, що непозиційні системи непридатні для практичного застосування в цифрових пристроях внаслідок своєї громіздкості і труднощі виконання арифметичних операцій.
З позиційних систем найбільш зручні однорідні системи числення, оскільки однорідна основа, тобто однакова кількість символів у всіх розрядах приводить до найбільш раціонального використання обладнання і найбільш простих алгоритмів виконання арифметичних операцій. Тому проаналізуємо однорідні позиційні системи числення на предмет їх застосування в цифрових пристроях. При цьому будемо враховувати наступні чинники:
• можливість простого і однозначного представлення чисел в заданому діапазоні;
• простота виконання арифметичних операцій і швидкодія цифрових систем;
• економічність системи, тобто простота технічної реалізації цифрової системи.
Таким чином, задача вибору системи числення для застосування в цифрових пристроях і МП зводиться, по суті, до задачі вибору раціональної величини основи системи р. Тому розглянемо з вказаних вище позицій системи числення із різними основами.
Однозначність представлення чисел у заданому діапазоні визначається необхідною розрядністю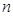 
представлення максимально можливого числа 
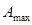. З урахуванням (1.6) для цілих чисел можна отримати:
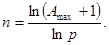
Будь-який із символів, що застосовуються для запису чисел, повинен зображатися у вигляді одного або декількох станів якогось фізичного елемента. Очевидно, що елемент буде тим простішим, чим менше станів йому потрібно мати, тобто чим менше основа системи числення. Наприклад, для реалізації двійкової системи числення можна застосувати реле, конденсатори, магнітні, напівпровідникові елементи тощо.
Трійкову систему числення можна ще реально реалізувати при допомозі конденсаторів і магнітних елементів, а р-позиційні елементи (при р > 3) носять штучний характер і при збільшенні р їх реалізація ускладнюється. Так, для реалізації десяткового елемента потрібно використати не менше 10 транзисторів.
Таким чином, по цьому критерію найбільш придатною для використання в цифрових пристроях є двійкова система числення.
Знайти оптимальне значення основи системи числення (з точки зору економічності основи системи числення) досить складно, оскільки, чим більше основа, тим менше кількість розрядів і, значить, елементів потрібно для зображення числа, однак тим більшу кількість символів повинен відображати кожен елемент, тобто мати більшу кількість стійких станів, що призводить до його ускладнення.
Для оцінки економічності системи числення як критерій виберемо кількість цифро-розрядів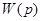 
, необхідну для зображення числа в i-й системі числення, виходячи з умови, що 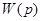пропорційнекількості деталей обладнання, тобто
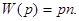
Правомірність останнього твердження зумовлена тим, що, наприклад, при виконанні операції множенні час множення на один розряд пропорційний основі р, а на всі 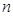розрядів-величині (
).
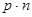З урахуванням (2.1) отримаємо:
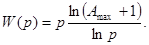
Припускаючи (умовно) безперервність функції 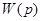, можна обчислити
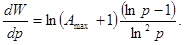
Із (2.4) витікає, що функція 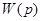досягає мінімального значення при 
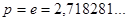(е – основа натурального логарифму).
З урахуванням необхідності застосування цілих значень числа р з останнього виразу можна визначити, що найбільш оптимальними є двійкова і трійкова системи числення, а
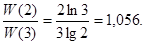
Однак в сучасних цифрових системах використовується в основному двійкова система числення. Це визначається простотою схемних рішень цифрових елементів, які можуть знаходитись в двох станах (включено/виключено), (це можна трактувати, як значення цифр двійкової системи числення).
Порівняння десяткової і двійкової систем числення показує, що остання є в 1,5 рази економнішою, ніж десяткова:
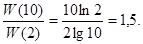
Необхідно також звернути увагу на той факт, що двійково-десяткове кодування є біль продуктивним, ніж кодування двійкове. Продуктивність кодування при різних основах систем числення можна порівняти, визначаючи число бітів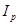 
, необхідних для представлення довільного числа в діапазоні (
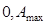) в системах числення з різними основами.
При безпосередньому двійковому кодуванні
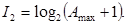
При двійковому кодуванні в системі числення з основою р
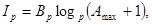
де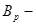 
кількість бітів, необхідних для однозначного представлення (кодування) цифр заданої системи числення.
З урахуванням (2.5) і (2.6) можна записати:
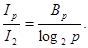
Для р = 10 і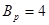 
(наприклад, для кодів 8421, EXCESS-3 тощо) отримаємо:
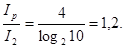
Це означає збільшення приблизно на 20% кількості бітів, необхідних для представлення десяткових чисел в двійково-десяткових кодах (4 біти для кожної цифри) у порівнянні з двійковими кодами вказаних цифр.
Перевагами двійково-десяткової системи відносно двійкової є:
• відсутність необхідності переведення початкових даних і результатів розрахунків з однієї системи в іншу; зручність контролю проміжних результатів шляхом виведення на індикацію для візуального спостереження;
• більш широкі можливості для автоматичного контролю через наявність в двійково-десятковому коді надмірних комбінацій.
Перевагами двійкової системи числення відносно двійково-десяткової є:
• економія близько 20 % обладнання;
• майже в 1,5 рази більш висока швидкодія;
• спрощення логічної побудови і значна економія обладнання в схемах управління і у допоміжних ланцюгах.
Математичним апаратом для аналізу і синтезу обчислювальних пристроїв, що дозволяє відносно просто і економічно будувати вузли і блоки, є алгебра логіки. Найбільший розвиток і закінченість вивчення, внаслідок своєї простоти і широкого практичного застосування, отримала двійкова логіка. При цьому всі арифметичні і керуючі ланцюги можна будувати на основі двійкових елементів, застосовуючи для їх аналізу і синтезу один і той же математичний апарат, що значно полегшує проектування схем цифрових пристроїв. Ця обставина також дозволяє зробити висновок на користь двійкової системи числення у порівнянні з іншими системами.
Таким чином, виходячи з перерахованих критеріїв, найбільш прийнятною для застосування в цифрових пристроях є однорідна позиційна система числення з основою, яка дорівнює двом. Однак в деяких конкретних випадках при синтезі обчислювального пристрою якому-небудь критерію може надаватись більше значення, ніж іншим. Тоді для застосування вибирається система числення, оптимальна за вибраним критерієм. Наприклад, в деяких випадках перевагу віддають десятковій системі числення, керуючись при цьому не міркуваннями економічності вибираного числення, а зручністю спілкування людини з цифровим пристроєм.
Двійкову систему числення застосовують у великих і середніх ЕОМ і ПЕОМ, призначених для вирішення науково-технічних задач, для яких характерний великий об’єм обчислень і порівняно малий об’ємпочаткових даних і результатів обчислень. Її також доцільно застосовувати в ЕОМ, призначених для управління технологічними процесами.
Двійково-десяткову систему числення застосовують для вирішення економічних задач, які характеризуються великим об’ємом початкових даних, порівняльною простотою і малим об’ємом перетворень, що виконуються над ними і великою кількістю результатів обчислень. Цю систему доцільно також застосовувати в калькуляторах і ЕОМ, призначених для інженерних розрахунків, а також в персональних ЕОМ.