Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
3.4 Точність подання чисел в цифрових пристроях
При рішенні різних задач потрібна різна точність кінцевих результатів. Так, при рішенні інженерних задач достатня точність до (3 – 4) десяткових знаків (10 – 13) двійкових), при рішенні наукових задач – до (8 – 9) десяткових або (25 – 30) двійкових знаків, а при рішенні особливо точних задач – до (15 – 20) десяткових, тобто (50 – 60) двійкових розрядів.
При обмеженій довжині машинних слів множина чисел, які можна подати в цифровому пристрої, є кінцевим. Тому подання чисел в цифрових системах, як правило, спричиняє за собою появу похибок, величина яких залежить як від форми подання чисел, так і від довжини розрядної сітки. Необхідно зазначити, що запас точності в цифрових системах береться звичайно в 1,5-2 рази більший, ніж це необхідно, що зумовлено крім всього іншого накопиченням похибок в ході обчислень.
Точність подання числа характеризується абсолютною і відносною похибками.
Абсолютна похибка ‒ це різниця між істинним значенням вхідної величини А і її значенням, отриманим з машинного зображення [А]
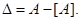
Усереднена абсолютна похибка подання чисел в цифрових пристроях з фіксованою комою визначається, як середня арифметична між мінімальним числом, яке може бути подано в даній розрядній сітці, і його мінімальною втратою. Якщо кома фіксована перед старшим розрядом, то абсолютна похибка дорівнює:
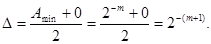
Тобто в машинах з фіксованою комою абсолютна погрішність постійна і дорівнює половині молодшого розряду.
Відносна похибка подання чисел визначається, як відношення усередненої абсолютної похибки до самого числа:
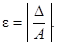
Оскільки саме число А міняється в межах
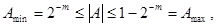
те і відносна погрішність є величиною змінною, що міняється відповідно в межах
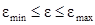
Для цифрових пристроїв з фіксованою комою вона визначається таким чином:
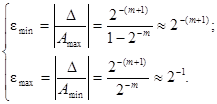
Таким чином, відносна похибка для машин з фіксованою комою залежить від величини числа і коливається в межах від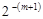 
для великих чисел, до 
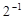для малих чисел.
В цифрових пристроях з плаваючою комою абсолютна похибка подання числа визначається таким чином:
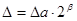
де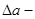 
похибка подання мантиси, яка визначається так само, як і абсолютна похибка подання чисел в пристроях з фіксованою комою, тобто 
, 
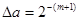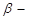порядок числа, який змінюється в межах
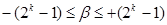
Отже, на відміну від цифрових пристроїв з фіксованою комою, в пристроях з плаваючою комою абсолютна похибка подання чисел залежить від порядку числа: похибка мінімальна при найбільшому від’ємному порядку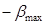 
і максимальна при найбільшому додатному порядку 
.
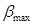Мінімальне і максимальне значення абсолютної похибки визначаються таким чином:
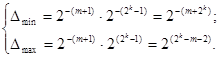
Відносна похибка подання чисел в цифрових пристроях з плаваючою комою визначається за загальним правилом:
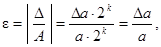
тобто не залежить від порядку числа і змінюється в межах:
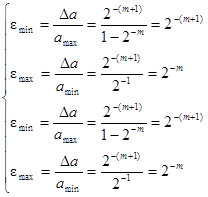
Отже, в цифрових пристроях з плаваючою комою, на відміну від пристроїв з фіксованою комою, відносна похибка зображення чисел у всьому діапазоні подання практично постійна і для чисел з нормалізованою мантисою залежить від кількості розрядів мантиси: чим їх більше, тим менше похибка подання.
У деяких обчислювальних засобах інформаційною одиницею є не окремі числа, а їх блоки або масиви, тобто послідовності, що складаються з сотень і тисяч чисел. У цих випадках нерідко застосовується проміжна форма поданя чисел, так зване представлення з поблочно плаваючою комою, при якому всьому масиву чисел привласнюється загальний порядок і масив вважається нормалізованим, якщо хоч би одне його слово є нормалізованим. Природно, що відносна похибка подання окремих елементів масиву буде при цьому різною. Як і у разі подання з фіксованою комою, максимальний по абсолютній величині елемент буде заданий з мінімальною похибкою, в той час як мінімальний по абсолютній величині елемент масиву – з максимальною відносною похибкою. Однак це не має істотного значення, оскільки основне інформаційне навантаження в цих випадках несуть максимальні елементи масивів. Разом з тим завдяки поданню чисел з поблочно-плаваючою комою вдається при прийнятній точності обчислень значно скоротити об’єм обладнання, а головне – час виконання операції, оскільки дії над порядками в цьому випадку виконуються тільки один раз за час обробки всього масиву чисел.
З цього витікає, що не можна віддати перевагу якій-небудь одній формі подання чисел. Звичайно в обчислювальних машинах загального призначення застосовують нормальну форму. Цим забезпечується великий діапазон подання чисел, висока точність обчислень, простота програмування. Ускладнення апаратури цих машин має другорядне значення.
В мікропроцесорах і спеціалізованих ЕОМ частіше застосовують фіксовану або поблочно-плаваючу кому, якщо інформація обробляється окремими масивами, оскільки ці форми забезпечують простоту конструкції цифрової системи. Програма для реалізації алгоритмів обчислень складається тільки один раз, діапазон зміни величин відомий заздалегідь, масштабні коефіцієнти підбираються один раз, необхідна точність обчислень також відома заздалегідь і визначає довжину розрядної сітки.
В сучасних ЕОМ використовуються обидві форми подання чисел. При цьому в більшості випадків формат чисел з фіксованою комою служить для подання цілих двійкових і десяткових чисел і виконання операцій над ними, що, наприклад, необхідно для операцій над кодами адрес (операції індексної арифметики).
В режимі з плаваючою комою звичайно використовується система числення з основою 16. У цьому випадку число А вважається нормалізованим, якщо хоч би один з чотирьох старших двійкових розрядів відрізняється від 0. Це дещо зменшує точність подання чисел, але дозволяє різко збільшити діапазон чисел, що подаютья в машині і прискорити виконання деяких операцій, зокрема нормалізації, оскільки зсувмантиси проводиться відразу на 4 розряди. При цьому кожний зсув мантиси на 4 розряди ліворуч або праворуч вимагає відповідної зміни порядку шістнадцяткового числа всього лише на одиницю.
Точність подання в цьому випадку підвищують за рахунок використання формату подвійної довжини (подання з подвоєною точністю)