Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

7.4 Контроль арифметичних операцій

Як відомо, арифметичні операції виконуються в ЕОМ в прямому, зворотному і додатковому кодах. Якщо зображення чисел зберігаються в машині в відповідному коді, те їх можна розглядати як єдині кодові комбінації, до яких можна застосовувати всі що формулювалися вище правила отримання пакунків. При цьому вимагається обов'язкова кратність загального числа розрядів вибранному модулю.

При додаванні в прямому коді складаються тільки цифрові частини зображеннь чисел, а знаки обробляються окремо. Тому в цьому випадку можливий контроль двома способами:

1) роздільний контроль знакової і цифрової частин зображеннь результату;

2) узагальнений контроль всього зображення. При роздільному способі контроль знакових розрядів роблять звичайно за допомогою схеми, що виявляє переповнення, бо в коді, що модифікувався поява одиночної помилки в знакових розрядах призводить до незбігу інформації в них. Для цифрових частин зображеннь маємо

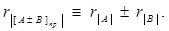
При узагальненому способі контролю вимагається корекція контрольного коду результату внаслідок того, що знак результату при додаванні чисел з рівними знаками повторює знак доданків, тобто контрольний код суми буде рівний

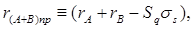
де S_q − значення знакового розряду операндів; s_s − вага старшого розряду свертки.

Приклад. Задані [А]_пр = 1,01101011; [B]_пр = 1,00110010; p=7. Знайти .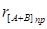

Маємо: r_a = 110; r_B = 101; [A + В]_пр= 1,10011101; 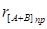= 111.

На основі (7.19) отримаємо

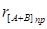 = 110+101 - 1 • 100 º 111(mod 7).

Узагальнений спосіб може бути застосований і для контролю виконання операції додавання в зворотному коді. В цьому випадку

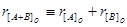
Приклад. Задані [А]_o = 1,011001001; [В]_o = 0,110001111; р = 3. Знайти .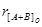

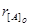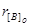Розв’язок: = 10; = 11; [A+B]_o = 0,001011001; 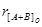= 10.

Перевірка:

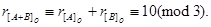
При додаванні чисел в додатковому коді необхідна корекція контрольного коду результату в випадку, якщо виникає одиниця переносу зі знакового розряду, тобто контрольний код суми буде рівний

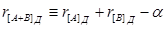
де a — корекція (a = 1, якщо виник перенос із знакового розряду, і a = 0, якщо переносу немає).

Приклад. Задані: [А]_д = 1,00110001110; [В]_д = 1,11101110111;  р = 15. Знайти 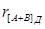. Розв’язок:  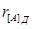= 0001;  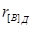= 1110; [A+B]_д= 1,00100000101; 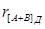= 1110 (mod 15).

Перевірка:

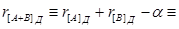0001 +1110— 0001 º 1110 (mod 15).

В зв'язку з алгебраїчним додаванням чисел в інверсних кодах виникає питання про перетворення контрольного коду при перетворенні прямого коду чисел в інверсний і назад. Для конкретності будемо вважати, що негативні числа зображаються в зворотному коді і р = 2^S - 1.

Нехай до перетворення в регістрі зберігався код

[A]_пр=2ⁿ+|A|

тобто в знаковому розряді була записана 1 (числа умовно цілі). Після перетворення цього коду в зворотний в регістрі отримаємо код

[А]_о=2ⁿ+(2ⁿ-1-|A|),

Виразив [A]_о через [A]_пр, одержимо

[A]_o=3•2ⁿ-1-[A]_пр=2[A]_пр+2(mod 3)

При перетворенні прямого коду в зворотний (або навпаки) необхідно виконати такі ж перетворення з контрольним кодом, тобто

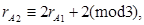
де 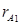 − контрольний код до перетворення;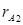− контрольний код після перетворення.

Таким чином, при виконанні операції алгебраїчного додавання в зворотному і додатковому кодах обробка основних і контрольних кодів може робитися в двох різних суматорах паралельно, що дозволяє в значному ступені розпаралелити процеси в основному і контрольному АУ, спростити алгоритми арифметичних операцій і зменшити час їхньої реалізації. При додаванні у зворотному коді суматори працюють незалежно один від одного при додаванні в додатковому коді одиниця переносу зі знакового розряду суми використовується для корекції контрольного коду останньої.

При використанні позиційної системи счислення всі арифметичні операції зводяться до послідовності додаваннь кодів. Тому достатньо перевіряти тільки правильність всіх сум, одержуваних в машині (остаточних при алгебраїчному додаванні і проміжних при множенні і діленні). Якщо формується 2n-разрядный результат, то операцію множення можна перевіряти також і прямим способом − порівнянням добутока залишків співмножників з залишком їхнього добутка.

Можливість порівняння основного і контрольного кодів перевіряється тільки після закінчення операції. При цьому в кінці операції перевіряється можливість порівняння також основного і контрольного кодів операндів. Це зумовлене тим, що поодинока помилка в операнді може виявитися джерелом багаторазових помилок в результаті операції. Наприклад, помилка, яка викривила один розряд множеного при його зсуві, викличе серію невірних його передач в суматорі. Тому цю помилку можна виявити або тільки при перевірці всіх часткових добутоків, або шляхом перевірки відповідності основної і контрольної кодів множеного після закінчення операції.