Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

7.3 Контроль логічних операцій

До логічних операцій відносяться операції зсуву, логічного додавання і множення.

Нехай задане число А = a_na_n-1…a₁, що має контрольний код r_A=a_ks .... a_k1.

Позначимо код числа А, ссунутий ліворуч, через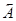 (без циклічного переносу) і через 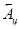з циклічним перенесенням (при зсуві праворуч стрілка в позначці буде повернута праворуч). Тоді контрольні коди можна позначити відповідно:

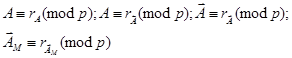
Зсув ліворуч на один розряд двійкового числа еквівалентно множенню його на два. Так як при зсуві числа відбувається втрата деяких його розрядів, то можна припустити, що контрольний код ссунутого числа зміниться на величину D:

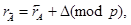
де 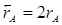 − ссунутий вліво контрольный код.

Величина А залежить від значень а_n і а_ks, що при зсуві виходять за межі розрядної сітки. Вихід старшої одиниці за межі розрядної сітки при зсуві n-разрядного числа еквівалентному видніманню a_ns_n+1одиниць з контрольного коду зсунутого числа, де s_n+1 − вага (n + 1)-го разряду.

Вихід за межі розрядної сітки розряду а_ks, = 1 при зсуві контрольного коду ліворуч еквівалентному його зменшенню на 2^S º 1 (mod (2^S - 1)), тобто цю втрату можна відновити доданням одиниці до контрольного коду. Тоді можна записати

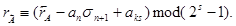
Ваги розрядів числа, наведеного в системі з основою 2^S, призначаються слідуючим чином, наприклад, при s = 3: розряди a_i:a_n a_n-1 a_n-2 a_n-3 a_n-4 a_n-5…a₃ a₂ a₁, вага s: 2² 2¹ 2⁰ 2² 2³ 2¹ 2⁰…2² 2¹ 2⁰, тобто s_n-1º 1(mod(2^S-1))

Внаслідок цього значення поправок D для виконання лівого зсуву по модулю (2^S-1) будуть такими, як в табл. 7.1.

Значення поправки D = -1 звичайно замінюють її доповненням по модулю р.

Для виконання зсуву ліворуч з циклічним переносом зі старшого розряду в молодший необхідно зменшити контрольний код на величину a_n (s_n+1 - 1). Так як s_n+1 º 1(mod р), то цей член рівний 0. Тоді можна записати

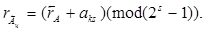
Приклад. Задане А = 1,01011010; s = 3; р = 7. Знайти 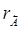 і .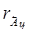

r_A= 101 Å 011 Å 010 ºº 011(mod7);

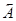= 0,1011010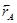0; =110.

Так як a_n = 1, а_ks= 0, то

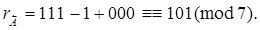
При циклічному зсуві 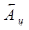 = 0,10110101. Тоді

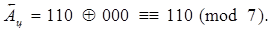
Таким чином, для того щоб не порушувалася відповідність між основним і контрольним кодами при циклічному зсуві на один розряд ліворуч, необхідно до зсунутого контрольного коду додати значення старшого його розряду, що він мав до зсуву. Для цієї мети служить ланцюг циклічного переносу з старшого розряду в молодший в суматору контрольного коду.

При зсуві праворуч відбувається втрата молодших розрядів числа і його контрольного коду. Контрольний код зсунутого праворуч числа можна отримати по формулі

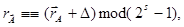
тільки поправка D буде при цьому інший.

В випадку простого зсуву поправка D до контрольного коду залежить від модуля р і для р=7 приймає наступні значення (табл. 7.2).

При зсуві, що модифікувався праворуч, який виконується по правилу А = 1, a_n-1 ... a₂a₁; 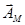== 1,1 a_n ... a₃a₂ Також відбувається втрата молодших розрядів кодової комбінації числа і контрольного коду. Для цього випадку контрольний код обчислюється по (7.13), але поправки D для р = 7 приймуть вигляд (табл. 7.3).

Приклад. Задане А = 1,01110111101; р= 7. Знайти 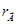 і .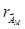

r_A = 101 Å 110 Å 111 Å 101 º 010 (mod 7);

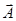=0,10111011110;  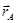= 001.

Так як а₁ = 1, a_k1 = 0, то D = 011. Тоді 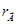 = 001Å011º100(mod 7)

Модифікований зсув числа А:

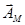= 1,10111011110.

При а₁=1; a_k1=0 поправка D=000. Тоді 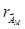=001Å 000=001(mod 7).

Таким чином, однім зі способів реалізації відповідності між основним і контрольним кодами при зсуві праворуч є корекція контрольного коду в відповідності з наведеної вище табл. 7.3.

Другим способом реалізації відповідності між основним і контрольним кодами при зсуві праворуч є подовження регістру основного коду на n розрядів, з тим щоб при зсуві праворуч не пропадали молодші розряди коду. При цьому здійснюється контроль по модулю р всього 2n-разрядного регістру основного коду.

Операцію додавання по mod 2 можна представити через інші операції, наприклад А Å В=А+В— 2 (A Ù В).

Це вираження можна уявити інакше:

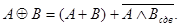
Тоді, використовуючи перехід від арифметичних виразів до порівнянь, отримаємо наступну формулу для утворення контрольного коду:

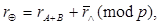
де r_A+B − контрольный код суммы двух чисел; 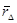 − інверсія контрольного коду логічного добутку двох чисел зі зсувом ліворуч на один розряд.

Приклад. Задані А = 010000111; В = 101110011; р = 7.

Знайти r_Å. Знаходимо: r_A = 010; r_B = 000; r_A+B = 0,10. Потім одержимо:

A Ù B = 0000000011: r_Ù = 011;

(A Ù B)_сдв = 0000000110; 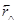 = 110.

Після цього визначимо 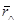 = 001 і по формулі (7.13) отримаємо

r_Å = 010 Å 001 º 011 (mod 7).