Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

7.2 Вибір модуля для контролю

Як було відзначене вище, справедливість властивостей порівнянь для контрольних кодів розповсюджується тільки на числовий спосіб контролю. В цьому складається його гідність. Гідність цифрового способу контролю полягає в простоті отримання контрольних кодів. Щоб зберегти обидва ці гідності, необхідно виконати умову

r_A=r’_A

Так як r_A ºº A (mod р);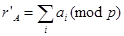, то в цьому випадку повинна виконуватись умова

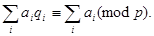
Це можливо тільки тоді, коли кожний елемент кожної з частин вираження рівний:

a_iq^j º a_i(mod p)

або

qⁱ º 1(mod p).

Звідси випливає, що

q º 1(mod p).

або

q = mp+1,

де m − ціле число.

Звідки одержуємо

тобто для збереження умови r_A = r’_A необхідно накласти певні обмеження на модуль р. До величини модуля звичайно подаються наступні вимоги:

1) величина модуля повинна забезпечувати викриття будь-якої з одинничних арифметичних або логічних помилок і якомога більшого числа помилок більш високої кратності;

2) утворення контрольного коду повинно здійснюватися найбільш простим і швидким способом, тобто простими засобами;

3) величина модуля р повинна бути по можливості невелика, з тим щоб залишки r від ділення на нього будь-яких чисел не вимагали великого обсягу обладнання для зберігання і обробки.

Аналіз (7.11) з урахуванням викладених вимог показує, що для двійкової системи счислення немає цілочисельного рішення. Тоді, з урахуванням того що цифрова інформація в ЕОМ представляється двійковими символами, для контролю доцільно перейти до систем счислення з основою q = 2^S, де s − деяке ціле позитивне число (s ³ 2). Цей перехід здійснюється розбиттям вхідної двійкової інформації на групи по s розрядів з наступним складанням цих груп по модулю р = (2^S - 1)/m або при m = 1, р = 2^S - 1. Цей процес називається коагулюванням числа по модулю р.

На практиці вміст контрольних розрядів, тобто пакунку двійкового числа визначається слідуючим чином:

1) все число, починаючи з молодших розрядів, розбивається на i=n/s груп по s розрядів кожна;

2) всі гурти послідовно, починаючи з молодшої, складаються на звичайному двійковому s-разрядном суматорі по модулю р=2^S - 1, тобто з циклічним переносом одиниці переповнення в молодший розряд (суматор зворотного коду). Отримана на суматору пакунку і буде цим залишком в двійковій системі счислення.

Розглянемо часткові випадки утворення пакунок при різноманітних значеннях модуля р.

1. Контроль по mod 3 (m = 1, s = 2, р = 3). Так як 2² º 1(mod 3), то контрольована інформація представляється символами четверичної системи, а пакунки утворяться складанням діад по модулю 3. Для цього вимагається двухрозрядний двійковий суматор з ланцюгом циклічного переносу з старшого розряду в молодший.

Приклад. Задані А = 53₁₀ = 110101₂; В= 30₁₀= 011110₂; р= 3.

r_A = 11 Å 01 Å 01 º 10(mod 3);

r_B = 01 Å II Å 10 = II (mod 3).

2. Контроль по mod 7 (m = 1; s = 3;  р = 7). Так як 2³ º 1(mod 7), то контрольована інформація представляється символами вісьмиричної системи, а для отримання пакунків необхідний трьохрозрядний двійковий суматор з ланцюгом циклічного переносу.

Приклад. Задане А = 249₁₀ = 011111001₂; р = 7.

r_A = 011 Å 111 Å 001 º 100(mod 7).

Можна показати, що з зростанням модуля підвищується корекційна спроможність однак при цьому росте обсяг контрольного обладнання.