Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

 

 

 7 КОНТРОЛЬ ВИКОНАННЯ ОПЕРАЦІЇ

 

7.1 Загальні положення

 

Контроль правильності виконання операцій може бути здійснений застосуванням спеціальних арифметичних кодів, ідея побудови яких базуються на властивостях порівняння по модулю.

Річ у тім, що при розгляді різноманітних арифметичних виразів вхідні числа, яці входять в ці вирази, можна замінювати на інші, порівняні із ними по вибраному модулю р. В частковості, кожне число може бути замінене своїм вирахуванням. При цьому всі машинні числа вважаються умовно цілими.

Розрізняють два способу отримання контрольного коду: числовий і цифровий. При числовому способі контролю контрольний код заданого числа визначається як найменший позитивний залишок від ділення числа А на вибраний модуль р:

 

 

rA = A - {A/p},

(7.1)

де {А/р} ‒ ціла частина від ділення числа А на р.

Величина модуля р істотно впливає на якість контролю. Якщо при числовому контролі р = q, де q ‒ основа системи счислення, в якій уявлена число, то контролюється тільки молодший розряд числа і контроль як такий не має сенсу. Для р = qm Справедливі аналогічні міркування, бо знов не всі розряди числа (при m<n) беруть участь в контролі і помилки в розрядах старше m взагалі не сприймаються.

Для числового способу контролю по mod р справедливі основні властивості порівнянь. Тому, якщо

 

A º rA(mod p);

B º rB(mod p).

(7.2)

де

0 £ rA £ p-1; 0 £ rB £ p-1; то A+B º rA + rB(mod p),

Звідки

 

rA+B º rA + rB(mod P).

(7.3)

Аналогічним образом доводиться справедливість і наступних співвідношень:

 

rA-B º rA - rB(mod p);

rAB º rArB(mod p).

(7.4)

Приклад. Задані А = 125; В = 89; р = 11. Знайти  rA(mod р) і rB(mod р).

rA == 125— {125/11} • 11 ºº 4 (mod 11);

rA= 89— {89/11} • 11ºº 1 (mod II).

 

Недоліком числового способу контроля по mod р є використання операції ділення для визначення залишку, що вимагає більших затрат машинного часу.

При цифровому способі контролю контрольний код числа утвориться діленням суми цифр числа на вибраний модуль при виконанні умов

 

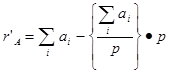 або 

(7.5)

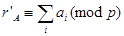
Можливі два шляхи отримання контрольного коду: 1) безпосереднє ділення суми цифр на модуль р; 2) складання цифр по mod р. Другий шлях значно простіше, бо якщо ai < р, то контрольний код одержується тільки операцією складання. В цьому полягає перевага цифрового способу контролю перед цисловим.

Приклад. Задані А = 153; В = 41; р = 11. Знайти r’A і r’B.

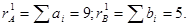
Однак при цифровому способі властивості порівнянь не завжди справедливі. Відбувається це із-за наявності переносу (позик) при виконанні арифметичних дій над числами. Тому отримання контрольного коду результату операція повинно супроводжуватися його корекцією.

Припустимо, задані числа А і В їхні контрольні коди

 

(7.6)

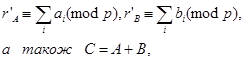
Вимагається знайти контрольний код 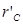. За наявності результату С код  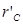знаходиться по загальному правилу:

 

(7.7)

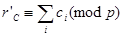
Для порівняння контрольних кодів необхідно отримати rC' через контрольні коди доданків.

Суму цифр результату можна знайти, знаючи цифри аi і bi і кількість переносу в кожному розряді. Кожний перенос уносить із одного розряду q одиниць, де q − основа системи счислення, і додає одну 1 в наступний розряд, тобто сума цифр зменшиться на величину (q-1) на кожний перенос. Тоді

 

(7.8)

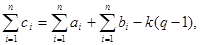
де k − кількість переносу, виниклих при додаванні. Таким чином

 

(7.9)

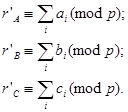
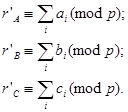
Підставивши ці значення в (7.8), отримаємо

 

r’C º [r’A+r’B-k(q-1)](mod p).

(7.10)

Аналогічні міркування можна навести і для різності чисел С = А - В.

 

Приклад. Задані А = 565; В = 278; р = 11. Знайти rC’ і rA+B’,