Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6.6 Переведення чисел в Д-кодах

Розглянемо переведення цілих десяткових чисел, наведених в Д-коді, в двійкову систему счислення.

Нехай задане десяткове число А = a_na_n-1…a₂a₁, де а_i ‒ десяткова цифра, що повинна бути представлена в Д-коді в вигдяді .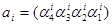

Використовуючи рівність 10 = 8+2 = (2³ + 2¹), будь-яке десяткове ціле число можна записати

A=(…(a₄ⁿa₃ⁿa₂ⁿa₁ⁿ)(2³+2¹) + a₄^n-1a₃^n-1a₂^n-1a₁^n-1) (2³+2¹)+

+…+a₄²a₃²a₂²a₁²) (2³+2¹)+ a₄¹a₃¹a₂¹a₁¹.

Множення на 2^k означає зсув двійкового коду на k розрядів ліворуч. Отже, переведення зводиться до зсуву відповідних тетрад і їхнього наступного складання.

Приклад. Задане А₁₀ = 254 або в коді Д1 А = 0010 0101 0100. Знайти А₂.

A₂ = (0010. (2³ + 2¹)+0101) (2³ + 2¹) + 0100 = (10000 + 0100+ +0101) (2³ + 2¹) + 0100 = 10. 000. 000+100. 000+1. 001. 000+ +10.010+0. 100=11. 101.000+10. 110=11. 111. 110.

Для переведення правильних дробів можна застосувати наступний прийом. Задану k-розрядний десятковий дріб спочатку розглядають як ціле число і переводять по описаному алгоритму, а після цього ділять на 10^k, записане двійковими символами (10^k можна перевести в двійковий код по тому ж алгоритму).

Приклад.Задане A₁₀=0,37 або в коді Д1 A=0,0011 0111. Знайти A₂.Рішення зображено на рис. 6.7.

Рисунок 6.7 – Рішення прикладу

Переведення чисел з двійкової системи счислення в Д-код може здійснюватися різними способами. Наприклад, діленням цілих двійкових чисел на число 1010. При цьому десяткові цифри одержуються послідовно одна за інший. При дробових числах ця операція видозмінюється таким чином, щоб при множенні на число 1010 можна було отримати відповідні цифри десяткових дробів.

Приклад. Задане A₂ = 0,0101111010 = 0,37₁₀. Знайти двійково-десятковий код цього числа. При визначенні коду кожної десяткової цифри числа множення А на 1010₂, Замінюємо додаванням А • 2³ і А • 2¹. Рішення зображено на рис. 6.8.

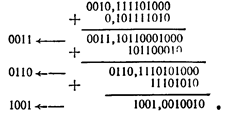
Ричунок 6.8 -  Рішення прикладу

Таким чином, A_2-10= 0,0011 0110 1001 = 0,369₁₀.

Переведення з Д-коду в двійкову систему счислення і навпаки можна спростити наступним чином. Нехай число А задане в коді Д1, тобто

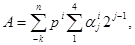
Позначивши через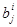 константи виду рⁱ2^j-1 одержимо

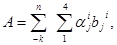
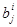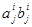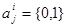Отже, якщо зберігати двійкові коди констант в таблиці, то переведення з Д-коду в двійкову систему зводиться до формування часткових добутоків виду, де, і їхнього наступного складання.

Приклад. В коді Д1 задане число А₁₀= 59, т. е. A_2-10= 0101 1001. Знайти двійковий код цього числа. Константи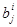 в цьому випадку наступні:

Тому

А₂=0 • 1010000+1 • 101000+0 • 10100+1 • 1010+

+1 • 1000+0 • 0100 + 0 • 10 + 1  • 1 = 111011.

Ці ж константи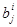 дозволяють спростити переклад числа А з двійкової системи счислення в Д-код. При цьому спочатку з числа А віднімається найбільша константа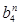. Якщо різниця позитивна, то  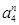= 1, в противному випадку 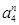= 0. На наступному кроці з залишку віднімається наступна константа 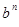, а значення  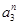визначається знаком нового залишку. Ця процедура повторюється до тих пір, доки не будуть знайдені всі 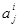. Слід відзначити, що при негативному, поточному залишку до нього на наступному кроці нова константа додається.

Приклад. Задане А = 59₁₀ = 111011₂. Знайти представлення числа А в коді Д1. В даному випадку n = 1, тому зажадаються тільки константи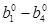 і 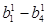, за допомогою двійкових кодів яких за 8 кроків отримаємо всіх вісем коефіцієнтів:

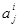    0111011

1-й крок  ¾   1010000

¾         010101 Зсув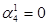 

2-й крок    +   101000

10011 Зсув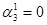 

3-й крок   —    10100

—                            00001 Зсув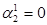 

4-й крок      +     1010

+     1001 Зсув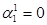 

5-й крок    —    1000

+     0001 Зсув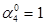 

6-й крок    —     100

—       011 Зсув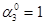 

7-й крок     +        10

—                 01 Зсув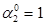 

8-й крок     +            1

00 Зсув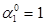 

Таким чином, A_2-10=0101 1001.

Перевагою даного способу переведення є використання одних і тих же констант для прямого і зворотного перетворень, що спрощує його апаратурну реалізацію. При цьому переведення в Д-код зводиться по суті до виконання операції ділення з змінним дільником, а переведення з Д-коду ‒ до виконання операції множення з змінним множеним.