Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6.5 Ділення чисел в Д-кодах

Ділення десяткових чисел звичайно виконується в прямих Д-кодах. Знак частки визначається так же, як і при двійковому діленні. Тому в подальшому розглянемо ділення позитивних десяткових дробів. З двох можливих способів ділення двійкових чисел для ділення десяткових чисел доцільно застосовувати тільки спосіб при непорушному дільникові і зсуву залишків і частки ліворуч. При двійковому діленні в кожному такті одержувалася чергова цифра частки, що приймала одне з двох можливих значень (0 або 1). Для визначення цієї цифри дільник віднімався з діленого на нульовому кроці і зсунутого ліворуч на один розряд чергового залишку на наступних кроках. При десятковому діленні кількість відніманнь дільника з зсунутого чергового залишку, як правило, більше 1, бо розряди частки можуть приймати значення від 0 до 9. Так же як і при множенні, на суматору ліворуч від крапки повинно бути п'ять двійкових розрядів: самий лівий ‒ знаковий, де фіксується знак залишку, і ще одна тетрада, в яку може зсуватися старша цифра поточного залишку при його зсуві ліворуч. Праворуч від крапки в суматорі повинна бути (n+1) тетрада, молодша з яких використовується тільки для округлення частки. В регістрі дільника праворуч від крапки повинно бути n тетрад. Регістр частки повинен бути з лівим зсувом і мати (n+1) тетраду. Причому молодша тетрада повинна являти собою реверсивний лічильник, в якому формується чергова десяткова цифра частки при виконанні чергового кроку ділення. Всіх циклів ділення повинно бути n+2, бо в першому циклі одержується цифра ліворуч від крапки, а праворуч від крапки необхідно сформувати n+1 цифру з урахуванням розряду округлення. Якщо на першому кроці цифра частки не рівна 0, то частки вийшла за межі розрядної сітки, тобто операція не коректна. При виконанні кожного кроку ділення до лічильника тактів додається 1, а операція завершується після виконання (n+2) циклів.

В вхідному стані діленее знаходиться в суматорі, дільник ‒ в регістрі дільника, а регістр частки встановлений в стан 0. Ділення починається з виднімання дільника з діленого на нульовому кроці і з ссунутих залишків ‒ на наступних кроках. Виднімання на кожному кроку замінюється додаванням в додатковому Д-коді і робиться до тих пір, доки не отримається негативний залишок. При цьому кожний раз при отриманні позитивного залишку додається одиниця в спеціальний лічильник, де накопичується чергова цифра частки. Після цього здійснюється зсув залишку на чотири двійкових розряди і додання до нього дільника до тих пір, доки не отримається позитивний залишок. Кількість додаваннь (без останнього) є доповненням відповідної цифри частки до 9, яка заноситься в лічильник чергової цифри частки.

Таким чином, процес ділення складається з ряду послідовно перемінних циклів додавання і виднімання, що виконуються на суматорі, працюючому по правилам алгебраїчного додавання в відповідному Д-коді, і завершуються зсувом частки і залишків ліворуч на одну тетраду. При цьому в тетраду суматора ліворуч від крапки зсувається код з тетради праворуч від урапки, а вміст знакового розряду не міняється.

Приклад. Поділити число А = 0,154675 на число В = 0,55. Так як А < В, на нульовому кроку залишок повинен бути негативним, тобто операція коректна. Далі розглянемо тільки цифрову частину чисел:

1-ий крок зображено на рис. 6.3

Рисунок 6.3 – 1-й крок операції ділення

Залишок < 0. Зсув частки ліворуч і дільника праворуч (або залишку ліворуч). 2-ий крок зоражено на рис. 6.4

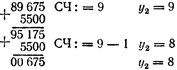
Рисунок 6.4 – 2-й крок операції ділення

Залишок > 0. Зсув частки ліворуч і дільника праворуч на 4 двійкових розряду. 3і-й крок зображено на рис. 6.5:

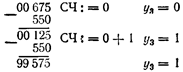
Рисунок 6.5 – 3-ій крок операції ділення

Залишок < 0. Зсув частки ліворуч і дільника праворуч на 4 двійкових розрядів. І так далі. Таким чином Y= А/В 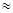 0,281.

По іншому способу при діленні чисел, заданих в Д-кодах, результат одержується в двійковій системі счислення.

Припустимо, при діленні А на В отримана частки у вигляді Y = 0, y₁y₂…y_n.

Тоді А = В(y₁2^-1 + у₂2^-2 + ... + y_n2^-n) + R_n де R_n ‒ залишок від ділення.

Покладемо R_n = 0 і y₁ = 1, y₂=y₃=…=0. Тоді залишок на першому кроці R₁=A ˗ 2^-1В.

Якщо R₁³ 0, то y₁ = 1; якщо R₁< 0, то y₁ = 0. В наступному випадку відновлюється попередній позитивний залишок. Після цього приймемо, що у₂ = 1, а інші y_i = 0 і т. д. Залишок на будь-якому кроці складе 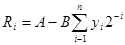. Слід врахувати, що при числах, наведених в Д-коді, необхідно вводити поправки. Тому для зберігання дільника бажано мати самостійний суматор, в якому при передачі одиниці з однієї тетради в іншу автоматично вноситься поправка.

Приклад. Задані А = 0,2425; В = 0,5200. Знайти Y = А/В. Рішення заданого прикладу зображено на рис. 6.6.

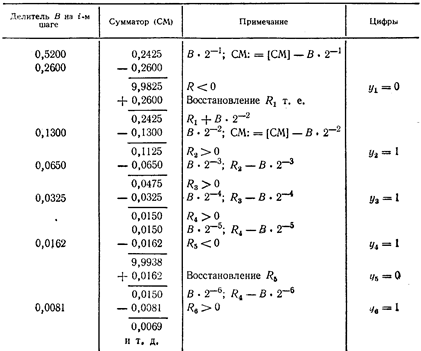
Рисунок 6.6 – Рішення прикладу

Таким чином, Y= 0,011101.