Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6.4 Множнення чисел в Д-кодах

Множення чисел в Д-кодах зводиться до послідовного складання часткових добутків, одержуваних при множенні множеного на чергову цифру множика. При цьому множення супроводжується розшифровкою значення черговий i-й тетради множника, що представляється в вигляді (b₄b₃b₂b₁)_i, і зсувом множника на чотири розряди одразу.

Самим простим засабом розшифровки тетради є послідовне виднімання одиниці з значення тетради до отримання нуля і відповідно додання множеного в суматор на кожному такті. Бо при множенні множеного на тетраду можливо переповнення разрядної сітки суматора (внаслідок того що множене додається до суми часткових добутків стільки раз, скільки одиниць міститься в даному десятковому розряді множника), то в ньому необхідно передбачити додаткову тетраду для врахування переносів, що виникають. З чотирьох можливих засобів множення в двійково-десятковій системі доцільно застосовувати тільки один: множення молодшими розрядами множника зі зсувом суми часткових добутків праворуч. Множення звичайно робиться в прямому коді, тобто знак результату визначається сумою цифр співмножників по модулю 2.

Приклад. Помножити в прямому Д2 коді числа

А = -0,45; [А]_пр=1,0111 1000;

В =+0,24; [В]_пр= 0,0101 0111.

Знак результату визначається так же, як і в випадку двійкової системи: 1 Å 0 = 1. Для виконання операції множення необхідний трьохтетрадний суматор. На рисунку 6.1 зображена операція множення.

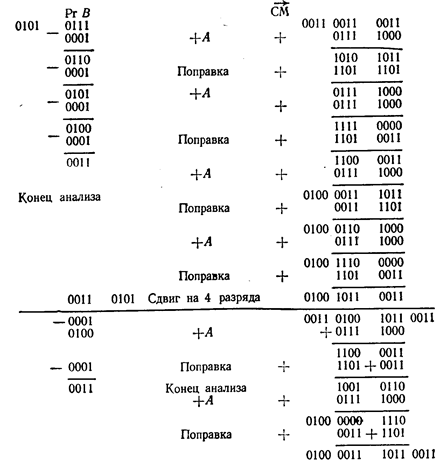
Рисунок 6.1 – Операція множення

Таким чином, [А • В]_пр= 1,0100 0011 1011 0011.

Якщо співмножники мають по n десяткових розрядів, то в регістрі множеного повинно бути n розрядів (тетрад) праворуч від крапки, а в суматорі повинно бути n основних розрядів, одна тетрада переповненнь і один (n+1)-й додатковий десятковий розряд (ДДР), що напередвизначений для округлення результату (в коді Д2 для округлення достатньо мати один додатковий двійковий розряд). При необхідності зберегти всі 2n розрядів добутку праворуч від суматора повинен бути ще зсунутий регістр для молодших розрядів добутку. Регістр множника повинен мати n тетрад праворуч від крапки. Причому, якщо молодша тетрада цього регістру виконана в виді реверсивного лічильника, тобто лічильнка, який може додавати або віднімати одиницю, то операцію множення можна прискорити в середньому майже в два рази. В цьому випадку необхідно мати спеціальний розряд для запису 1, якщо при складанні в лічильнику-тетраді з'явиться код 10₁₀.

Такий склад обладнання пояснюється слідуючим чином. Якщо чергова цифра множника, яка знаходиться в молодшій тетраді (лічильникові) регістрі множника, рівна або менш 5₁₀, то робиться багаторазове додання множеного до суми часткових добутуів суматора. При кожному складанні множеного віднімається 1 з лічильника. Такі дії виконуються до тих пір, доки на лічильникові не з'явиться код 0. Якщо ж чергова цифра множника рівна або більше 6₁₀, то робиться багаторазове віднімання (додавання в додатковому Д-коді) множеного з суми часткових добутків суматора. При кожному відніманні множеного до вмісту лічильника додається 1. Виднімання тривають до тих пір, доки в лічильникові не з'явиться код 1010. При цьому в спеціальний розряд записується 1.

По закінченню аналізу поточної тетради множника робиться зрушення на одну тетраду праворуч суми часткових добутків і множника. При цьому в лічильник регістру множника зсувається наступна тетрада множника, до якої додається вміст спеціального розряду, тобто 1, якщо вона була там записана. Операція множення закінчується зсувом множника і суми часткових творів. Всього повинно бути виконане n зрушень. На останньому зсуві в лічильник зсувається нуль множника. Якщо при цьому в нього додається 1 зі спеціального розряду, то операція множення закінчується доданням множеного до суми часткових добутків. В результаті одержується 2n-разрядний добуток.

Таким чином, описаний алгоритм дозволяє істотно скоротити час множення практично без модифікації складу обладнання. Якщо необхідний n-розрядний результат, то й твір округляється шляхом додання до ДДР, тобто до (n+1)-й тетради, числа 510.

Приклад. Задано A=0,367₁₀, B=0,583₁₀. Знайти добуток С=АВ і округлити до 3-х розрядів. Всі дії для простоти виконуємо в десятковому коді. Квадратною рамкою обведений лічильник в регістрі множника (Рг B), лічильник тактів (розрядів) множення (СЧТ) і спеціальний розряд (СПР). На суматору (СМ) самий лівий розряд (від крапки) ‒ двійковий (знаковий), а другий ліворуч (розряд переповнений) ‒ десятковий. Оперція множення зображена на рис.6.2.

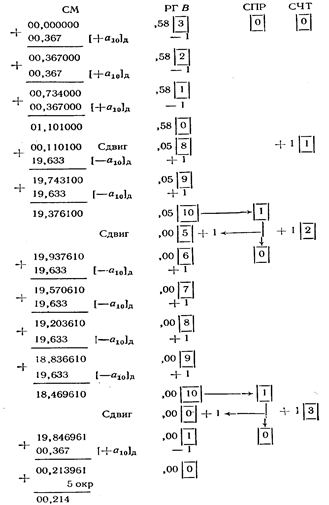
Рисунок 6.2 – Операція множення

Таким чином, С = А • В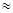 0,214₁₀.

Подальшим розвитком описаного способу прискорення операції множення в Д-кодах є формування кратних множеного А. Наприклад, за наявності кратних ±2A і ±4A часний добуток формується слідуючим чином в залежності від поточної цифри множника В (табл. 6.2).

При цьому, якщо попередня цифра В була більше п'яті, то дію на черговому кроку треба збільшити на +1A. Як видно з таблиці, в гіршому випадку для даного способу зажадається всього 2 дії алгебраїчного додавання при отриманні одного часткового добутоку, а в середньому для цього необхідно 1, 2 додаваннь ‒ відніманнь. Спосіб дозволяє аналізувати чергову цифру множника простими апаратними засобами. Для його реалізації зажадається ще два регістри для зберігання 2A і 4A або комутатор для формування 4A і 2А шляхом зсуву А відповідно на 2 і 1 розряд

Інший прийом, що застосовується для прискореного множення, зводиться до наступних покрокових перетворень добутків:

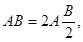 якщо B-парне число;

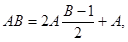 якщо В-непарне число.

Приклад. Задано А = 35, В = 34. Знайти С = А • В.

35 • 34 = 2 • 35 • 34/2 = 70 • 17 = 140 • 8 + 70 = 280 • 4 + 70 = 560 • 2+70 = 1 120 • 1+70 = 1190.

Таким чином, С=А • В= 1190.

При цьому подвоєння числа означає його зсув ліворуч, а ділення на 2 ‒ зсув праворуч. Бо двійкові ззуви робляться над двійковими кодами, то вимагається корекція тетрад на кожному кроці. Як бачимо, додавання роблять тільки при непарному множнику. Найбільша їхня кількість можлива при В = 2_n ˗ 1 і дорівнює (n ˗ 1), а при В = 2ⁿ роблять тільки зсув множеного і множника.

Якісну оцінку ефективності розглянутих способів множення дасть порівняння числа додавань, що необхідні для отримання повного добутка по кожному з способів, наприклад, при В = 0,583:

1. Тільки складання множеного. Кількість додавань: 5 +8+3= 16.

2. Складання і виднімання множеного, що при цьому практично має вигляд В = 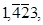 де риска над цифрою означає віднімання. Тоді кількість додавань складе: 1+4+2+3 = 10.

3. Складання і виднімання кратних множених. Кількість додавань: 2+1+2 = 5.

4. Покрокове формування добутока шляхом двійкового зсуву множеного і множника. Кількість додавань: 1+1+1+1= 4.

Таким чином, якщо врахувати, що в реальних ЕОМ кількість розрядів значно більше трьох, то виграш в швидкодії при виконанні множення прискореними способами виявиться ще більш істотним.