Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6.3 Зсув Д-кодів

При зсуві Д-коду числа на один десятковий розряд необхідно передбачити зсів двійкових цифр відразу на 4 розряду. Правила зсуву залишаються тими ж, що і для двійкових дробів, тобто зсув праворуч обмежується величиною допустимої помилки, яку можна зменшити шляхом округлення зсунутого числа. Для цього вводять додатковий десятковий розряд (ДДР). При цьому позитивні дроби округляють доданням числа 5 в ДДР, якщо цифра в ньому більше або рівна 5. Округлення негативного дробу, наведеного в зворотних Д-кодах, не робиться. Округленне в додаткових Д-кодах робиться тільки тоді, коли хвост числа більше 0,5 х 10^-n, де n ‒ число основних десяткових розрядів. Операція зсуву Д-коду ліворуч коректна до тих пір, доки не відбудеться переповнення розрядної сітки (табл.6.1).

При виконанні операцій множення і ділення Д-кодів нерідко виникає необхідність множення або ділення чисел на 2. Для множення Д1 коду на 2 необхідно зсунути задане число на один двійковий розряд ліворуч. Поправки вносяться як і при додаванні в коді Д1, тобто якщо в i-й тетраді в результаті зсуву виникла заборонена комбінація або з i-й тетради в (i+1)-ю була висунута одиниця, то до 1-ї тетради додається поправка 0110 і ланцюг міжтетрадних переносів не блокується. В інших випадках корекція результату не робиться.

Приклад. Задане в коді Д1 число А=0.159₁₀=0.0001 0101 1001. Зсунути його на один двійковий розряд ліворуч

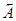=0,    0010  1011 0010

+ 0110 +        0110

0, 0011 0001  1000

Таким чином, 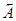= 0,0011 0001 1000 = 0,318₁₀.

Приклад. Задане в коді Д1 число A=0.15810=0.0001 0101 1000. Зсунути його на один двочный розряд праворуч

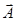=0,    0000  1010 1100

+ 1101 +        1101

0, 0000 0111  1001

Таким чином, 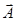 == 0,0000 0111 1001 = 0,079₁₀.

При діленні коду Д1 на 2 необхідно зсунути його на один двійковий розряд праворуч і відняти поправку 0011 з тих тетрад, в які зсунулася одиниця з попередньої або додати поправку 1101 з блокуванням міжтетрадного переносу, що виникає.

При множенні коду Д2 на 2 необхідно зсунути його на один двійковий розряд ліворуч. Корекція вноситься як і при додаванні, тобто якщо з i-й тетради зсувається одиниця в (i+1)-ю, то до i-й тетради додається 0011, якщо ж одиниця в (i+1)-ю тетраду не зсувається, те до i-ї тетради додається 1101. При цьому ланцюги міжтетрадних переносів блокуються.

Приклад. Задане в коді Д2 число А=0.159₁₀=0.0100 1000 1100.

Зсунути його на один розряд ліворуч

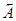=0,    1001  0001 1000

+ 1101 0011 0011

0, 0110 0100  1011

Таким чином, 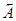 = 0,0110 0100 1011 = 0,318₁₀.

При діленні коду Д2 на 2 необхідно зсунути його на один двійковий розряд праворуч і додати поправку згідно табл. 6.1.

Табл 6.1 одержується на основі наступних міркувань. Якщо цифра а, записана в даній тетраді, парна, тобто а = 2 b, то її двійковий код буде непарним, бо він рівний а + 3 = 2b + 3. Якщо а ‒ непарне, тобто а= 2b +1, то двійковий код в даній тетраді буде парним, бо він рівний 2b + 4.

В старшу тетраду нічого не зсувається, але з неї в сусідню праворуч тетраду зсувається або 0, або 1 Якщо зсувається 0, значить а = 2b + 1, тобто код в ній парний і рівний 2b + 4. Після зсуву він стане рівний b + 2, а повинен бути рівним b + 3, отже, необхідна поправка на величину П₀= 0001. Якщо з старшої тетради зсувається 1, то а парне (а == 2b), і після зрушення повинен бути код b+3. Зсувається ж код —1/2(а+3) =1/2(2b+3) = b+1+1/2. Тут 1/2 переходить у вигляді 1 в тетраду праворуч, а поправка, очевидно, буде рівна П₁=0010.

Розглянемо зсув будь-який тетради. Якщо в неї зсувається 0, то це означає, те в неї повинна попасти 1 з вагою 5 (10/2). Якщо з тетради зсувається 0, то в ній число непарно, тобто а = 2b + 1, а код його парний, тобто рівний 2b + 1 + 3 = 2b + 4. Після зсуву в тетраді буде код b+2, а повинно бути b + 3. Тому поправка в цьому випадку складе П₀₀ = (5 + 1)₁₀ = 0110. Якщо ж з даної тетради зсувається код 1, то в ній число парне, тобто а = 2b, а код непарний і рівний 2b + 3. Після зсуву в тетраді отримаємо (2b+3)½ = b+1+½. При цьому ½ в вигляді 1 зсувається в сусідню праворуч тетраду, а в даній залишається код b + 1, то повинно бути b + 3. Звідси поправка дорівнює П₀₁ == (5+ + 2)₁₀ = 0111.

Якщо в дану тетраду зсувається код 1, те це означає, що в неї повинен попасти 0, бо десяткова цифра в попередній тетраді парна (цифра, а не її код!). Ця 1 має вагу 8, тому в поправку необхідно ввести негативну величину (-8). Якщо з даної тетради зсувається 0, то код в ній парний і рівний 2b + 4. Після зсуву він рівний b+2, тобто результуюча поправка повинна скласти 1 ˗ 8 = ˗7. Негативні поправки звичайно вносяться в вигляді доповнень до 16, тому П₁₀= 1001. Якщо з даної тетради зсувається 1, значить а парне, тобто а = 2b, а код в ній непарний і рівний 2b + 3. Після зсуву отримаємо код b + 1 + ½. При цьому ½ переходить в вигдяді 1 в сусідню праворуч тетраду, а в даній залишається b + 1, тобто необхідна поправка коду тетради на величину 2 ˗ 8 =  ˗6, що також задається в виді доповнення до 16, тобто П₁₁ = 1010. Необхідно пам'ятати, що в коді Д2 при реалізації поправок ланцюги міжтетрадних переносів блокуються.

Якщо дана тетрада молодша, то праворуч двійкова цифра, що зсувається з неї буде являти собою інверсний код залишку від ділення числа на 2: якщо цифра коду залишку 0, то цифра залишку числа рівна 1 і навпаки.

Приклад. Задане в коді Д2 А = 526₁₀ = 1000 0101 1001, Зсунути його на один двійковий розряд праворуч

A=        0100  0010 1100 1

0001     0111  1010

0101     1001  0110

Таким чином, 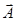 = 0101 1001 0110 = 526 : 2 = 263₁₀.