Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6.2 Додавання чисел в інверсних Д-кодах

Д-коди можуть бути представлені в розрядній сітці машини в формі або з фіксованої, або з що плаваючою крапкою. При цьому негативні числа можуть бути представлені в прямому, зворотному і додатковому кодах. Тому, якщо

А = 0,  a₁a₂…a_n, де а_i— тетради, то

[А]_пр= a₁a₂…a_n;

[A]_o==;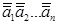

[A]_д==,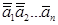

де a_i ‒ доповнення до р-1=9 в усіх тетрадах; 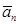‒ доповнення до р=10 в молодшій тетраді.

Отже,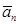 + a_i = р = 10;  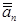+ a_i = р ˗ 1 = 9. Зворотній код Д2 одержується простим інвертуванням цифр тетрад.

Приклад. Знайти зворотний і додатковий коди числа

А = -0.136 для коду Д2.

A_Д2= -0,0100  0110 1001;

[A_Д2]_o =1 ,1011        1001 0110;

На основі співвідношення отримаємо додатковий код числа А:

[A_Д2]_д =1 ,1011        1001 0111.

В коді Д1 пряме інвертування цифр тетрад означає отримання доповнення до 2⁴ - 1 = 15. Тому для отримання зворотного коду числа в коді Д1 в увсі тетради числа додають спочатку +0110, після чого роблять інвертування цифр тетрад.

Приклад. Для числа A= 0,148 = 0,0001 0100 1000 отримати зворотний і додатковий коди Д1.

0,0001  0100  1000

0110     0110  0110

0,0111  1010  1110.

Звідси    [A_Д1]_o = 1,10000101 0001;

[A_Д1]_д = 1,100001010010.

Відзначимо, що додання 1 в молодший розряд при отриманні додаткового Д2 коду робиться значно складніше, ніж в коді Д1, бо ця операція виконується як звичайне додавання в Д2 коді. При додаванні в інверсних Д-кодах, як і при додаванні в прямих Д-кодах, необхідна корекція результату, що може здійснюватися або програмними, або апаратними засобами. На практиці звичайно застосовують другий засіб. При цьому в процесі виконання корекції ланцюга міжтетрадного переносу в суматорах блокуються для коду Д2, а при додаванні в коді Д1 не блокуються.

Приклад. Скласти в зворотному і додатковому кодах Д1 і Д2 числа

А = - 0,926 і В =+ 0,845.

Для коду Д1

А = - 0,1001 0010 0110 і В =+ 0,1000 0100 0101.

[A]_o=    1,0000        0111 0011

[B]_o=    0,1000        0100 0101

1,1000  1011  1000

+ 0110

[C]_o=[A]_o+[B]_o=      0,1001        0001 1000

[C]_пр=   1,0000        1000 0001

[A]_д=    1,0000        0111 0100

[B]_д=    0,1000        0100 0101

1,1000  0100  0101

+ 0110

[C]_д=    1,1001        0001 1001

[C]_пр=   1,0000        1000 0001

Для коду Д2

A= ˗      0,1100        0101 1001

B=+      0,1011        0111 1000

[A]_o=    1,0011        1010 0110

[B]_o=    0,1011        0111 1000

1,1111  0001  1110

+ 1101  0011  1101

[C]_o=              1,1100        0100 1011

[C]_пр=             1,0011        1011 0100

Негативні поправки вносяться в виді доповнення: 1101

Таким чином, код Д2, тобто код з надлишком 3, дозволяє надто просто формувати порозрядні доповнення до р ˗ 1 = 9, а також просто виконувати алгебраїчне додавання. Однак, як і код Д1, він вимагає корекції результату, що збільшує час реалізації операцій. Код Д2 володіє ще рядом корисних властивостей. Наприклад, цифри десяткової системи счислення, значення яких більше або рівні п'яті, відрізняються тим, що в старшому розряді двійково-десяткового коду завжди присутня одиниця. Завдяки цій властивості по значенню тільки одного старшого розряду тетради визначається необхідність округлення. Цією  ж властивістю можна скористуватися для спрощення реалізації прискореного множення.