Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

6 ДВІЙКОВО-ДЕСЯТКОВА АРИФМЕТИКА

6.1. Додавання в прямих Д-кода

В двійковому поданні десяткового числа, що кодувалося кожна десяткова цифра зображається тетрадою двійкових символів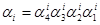, де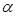, ‒ десяткова цифра 1-го розряду; 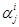‒ двійкова цифра 1-ї тетради. Отриманий таким чином десятковий код, що кодувався двійковими символами, для більш короткої назви вживають Д-кодом.

Є деяка множина Д-кодів. Вона зумовлюється наявністю всього 10 дозволених з 16 можливих комбінацій, що припускає тетрада. Наявність заборонених комбінацій в Д-кодах відрізняє їх від звичайних позиційных систем счислення, в яких всі комбінації ‒ дозволені. З всієї безлічі відомих Д-кодів найбільше розповсюдження в обчислювальній техніку отримали код Д1 прямого заміщення (система 8421) і код Д2 з надлишком 3 (система 8421+3).

Із-за заборонених комбінацій, при додаванні чисел в будь-якому з Д-кодів виникають необхідність в корекції результату і труднощі в формуванні десяткового переносу в наступну тетраду. Особливості додавання чисел в кожному з Д-кодів різноманітні, тому розглянемо їх окремо. При цьому будемо вважати, що задані числа A=a_na_n-1…a₁a₀ і B=b_nb_n-1…b₁b₀, де a_i, b_i ‒ двійково-кодовані десяткові цифри (тетради). Необхідно отримати:

А + В = С = c_n+1c_n…c₁c₀, Причому

C_i=a_i+b_i+П_i-1-П_ip; c_n+1=П_n

де П_i = {0, 1}, П_i-1 = {0, 1} ‒ десяткові переноси; р = 10 ‒ підстава системи счислення.

Бо найбільше десяткове однорозрядне число рівно 9, то з урахуванням переносу в даний розряд, значення результату розрядного складання лежить в межах від 0 до 19. При цьому одиниця в другому розряді являє собою десятковий перенос в наступну тетраду, а сума одержується в двійковому коді, відмінному від необхідного двійково-десяткового представлення,тобто Вона вимагає корекції.

Код Д1

При додаванні чисел в коді Д1 можуть виникнути наступні випадки:

1 Якщо а_i + b_i + П_n-i < 10, то при виконанні дій над розрядами тетради по правилам двійкової арифметики відразу одержується правильний результат.

1 Якщо а_i + b_i + П_n-i ³ 10, то виникає десятковий перенос. Тому сума в даній тетраді повинна бути рівна:

a_i+b_i+П_i-1-П_i•10,

де П_i = 1.

При цьому признаком невірного результату є в одному випадку виникнення потетрадного переносу П_i’ = 16, В другому-поява забороненої комбінації, якщо 15 ³ а_i + b_i + +П_i-i ³ 10. В будь-якому з цих випадків необхідно скоректувати результат в даній тетраді введенням поправки + 0110, що призведе до виникненню потетрадного переносу і в другому випадку. Корекція зумовлена тим, що кожний перенос виносить з собою з даної тетради 16 одиниць, а приносить в наступну тільки 10 одиниць.

Приклад. Скласти тетради а_i = 1000 і b_i = 1001 при П_i-1 = 1.

c_i’ = а_i + b_i + П_i-i = 10 010.

Так як П_i== 1, вимагається корекція результату

c_i= 0010 + 0110 = 1000;  П_i=П_i'=1.

Приклад. Скласти а_i = 1000 і b_i = 0110 при П_i-1 = 1.

c_i’ = а_i + b_i + П_i-i = 1111.

Так як величина с_i’ = 1111 належить до заборонених комбінацій, те необхідно ввести поправку виду 0110:

с_i= 1111+0110= 10101, т. е. П_i= 1, с_i=0101.

Таким чином, якщо в i-й тетраді сума цифр з переносом з (i-1)-й тетради менш 10, то додавання робиться без поправок; якщо ж сума цифр з переносом рівна або більше 10, те відбувається корекція результату тетради введенням поправки +0110, а при цьому перенос, що виникає додається до вмісту (i+1)-й тетради.

При цьому, якщо в декількох тетрадах, починаючи з (i+1)-й, розрядна сума рівна 1001, то перенос призведе до формування забороненої комбінації в (i+1)-й тетраді. В результаті цього зажадається корекція, що призведе до забороненої комбінації в (i+2)-й тетраді і т. п. Отже, із-за послідовного розповсюдження потетрадних переносів час додавання в коді Д1 складе в гіршому випадку n тактів, де n ‒ кількість тетрад. Звичайно схеми будують таким чином, щоб перенос, що виникає при доданні тетрадної поправки, минав скрізь тетради, в яких попередня сума рівна 9₁₀=1001₂ і скидав їх в 0. При цьому сума завжди формується за два такту.

Приклад. Скласти числа

А = 248₁₀ = 0010  0100  1000 і В = 349₁₀ = 0011  0100  1001

0010     0100  1000

0011     0100  1001

0101     1001¬       0001

0110

0101     1001  0111: 597₁₀=248₁₀+348₁₀

Стрілкою показані одиниці потетрадних переносів.

Код Д2

При додаванні чисел в коді Д2 можливі наступні випадки c врахуванням того, що а_i’ = а_i+3; b_i’ = b_i + 3, де а_i’ и b_i’‒ тетради для коду Д2.

Якщо а_i’+ b_i+П_i-1-1£15,  то   C_i=( а_i+ b_i+П_i-1+3)+3 = С_i + +6 = C_i’ + 3,

тобто результат необхідно скоректувати на величину (-0011). Якщо ж а_i+ b_i+П_i-1 - 1>15, то C_i=( а_i+ b_i+П_i-1+6) +10 - 16 = C_i’ - 3. Тут виникає десятковий перенос, що при переході в старшу тетраду міняє свою вагу з 16 на 10. Тому в цьому випадку вимагається поправка результату на величину +0011.

Суматори не роблять операцію виднімання, тому поправка (˗ З₁₀) = (˗ 0011)₂ здійснюється доданням в дану тетраду числа (13)₁₀ = (1101)₂ і блокуванням при цьому переносу, що виникає з даної тетради в старшу, яка має значення (16)₁₀ ˗ (10000)₂:

(˗3 = +13 ˗ 16)₁₀ или (˗0011 = +1101˗10000)₂.

Приклад. Задані в коді Д2

А = 46 = 0111 1001; В == 37 = 0110 1010.

Знайдемо суму

0111     1001

0110     1010

1110     0011

1101     0011

1 1011 0110 = 83

не реалізується

При додаванні в коді Д2 не виникає проблеми наскрізного переносу, і операція додавання виконується за два такти. Це пояснюється тим, що якщо в декількох тетрадах сума до додання поправки рівна 9₁₀ = 1111₂, то при надходженні переносу з (i ‒ 1)-й тетради в 1-ю, її вміст скинеться в 0 і перенос піде в (i+1)-у тетраду в цьому ж такті складання. В 1-у ж тетраду в другому такті складання буде додана поправка +0011. Тому корекція результату здійснюється потетрадно з блокуванням кіл потетрадних переносів. Таким чином, в коді Д2 завжди робиться корекція проміжного результату, отриманого шляхом додавання цифр доданків по правилам двійкової арифметики. При цьому, якщо при додаванні i-x тетрад не виникає переносу, тобто П_i = 0, то поправка рівна -0011. Якщо ж виникає потетрадний перенос П_i = 1, то поправка в 1-й тетраді дорівнює +0011.