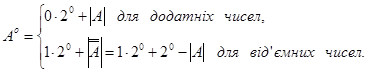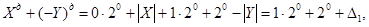Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
5.4 Виконання операцій алгебраїчного додавання в доповняльному коді
Як і в оберненому коді, при використанні доповняль-ного коду операція віднімання замінюється операцією алгебраїчного додавання. При цьому знаковий розряд і цифрова частина числа розглядаються, як єдине ціле, тобто з від'ємними числами цифровий пристрій оперує, як з неправильними дробами. Правильний знак суми формується автоматично в процесі додавання вмісту знакових розрядів операндів і одиниці перенесення з цифрової частини, якщо вона має місце.
Використаємо визначення доповнення до двох і доповнення до одиниці для форулювання загальних правил додавання двійкових операндів, представлених у формі з фіксованою комою (правильні дроби), в доповняльному коді. Розгляд будемо вести для двох основних варіантів:
а)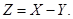
Обчислимо цей вираз із застосуванням доповнень.
Як відомо, для правильних двійкових дробів
|
|
Тоді
|
|
де 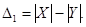
Розглянемо два такі випадки:
1) Якщо 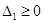 , то
, то 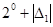 >
> 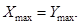
Це означає, що виникає перенесення до знакового розряду, і також, із знакового розряду. З метою отримання правильного результату необхідно не враховувати (відкинути) перенесення із знакового розряду. Тоді
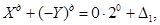
2) Якщо 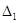 < 0, то
< 0, то 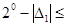
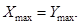
Це означає, що не виникає перенесення до знакового розряду, а, також, із знакового розряду.
Результат операції є від'ємний і записується в доповняльному коді так:
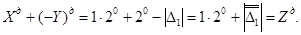
б)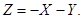
Обчислимо в доповняльному коді:
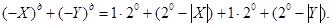
Вираз
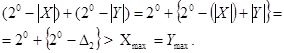
Це означає, що виникає перенесення до знакового розряду, і також, із знакового розряду.
Результат операції є від'ємний і записується в доповняльному коді так:
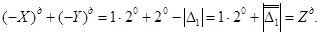
Отримані результати дають право зформулювати таке правило додавання двох чисел в доповняльному коді:
Наступні приклади ілюструють чотири основні варіанти додавання чисел у доповняльному коді при виконанні умови 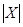 >
> 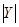 і
і 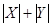 < 1.
< 1.
1) 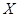 > 0;
> 0; 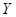 > 0;
> 0; 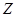 > 0;
> 0;
Приклад 1.
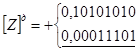 .
.
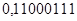
У звязку з тим, що доповняльний код додатніх чисел співпадє з записом самих чисел, оприманий результат співпадає з результатом додавання цих чисел у прямому коді.
2) 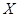 > 0;
> 0; 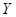 < 0;
< 0; 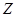 > 0;
> 0;
Приклад 2.
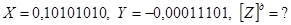

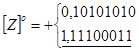
відкинути 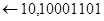
Виникає перенесення в знаковий розряд і із знакового розряду. Одиницю перенесення із знакового розряду необхіднр відкинути.
3) 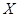 < 0;
< 0; 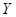 > 0;
> 0; 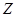 < 0;
< 0;
Приклад 3.
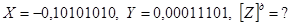

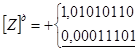
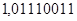
Сума від'ємна. Перенесення до знакового розряду немає. Перенесення із знакового розрядк теж немає. Результат правильний.
4) 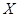 < 0;
< 0; 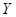 < 0;
< 0; 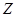 < 0;
< 0;
Приклад 4.
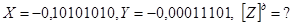

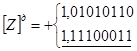
відкинути 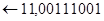
Сума від'ємна. Одиницю перенесення із знакового розряду необхідно відкинути.
Таким чином, у всіх випадках знак суми формується автоматично в результаті застосування загальних правил порозрядного додавання знаковиз і цифрових розрядів операндів Очевидно, що у всіх розглянутих випадках додавання операнди можна поміняти місцями, і при цьому результат не зміниться.