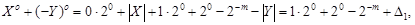Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
5.3 Виконання операцій алгебраїчного додавання в оберненому коді
В оберненому коді знаковий розряд і цифрова частина числа розглядаються, як єдине ціле, внаслідок чого цифрові пистрої виконують операції з від'ємними числами, які мають вигляд неправильних дробів. Правильний знак суми визначається автоматично в процесі додавання цифр знакових розрядів операндів (і одиниці перенесення з цифрової частини, якщо вона тає місце).
Характерною особливістю оберненого кода є наявність циклічного перенесення (якщо він виникає) із знакового розряду в молодший розряд цифрової частини, завдяки чому виконується корекція результату на 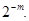 Це зумовлено тим, що додавання проводиться за модулем
Це зумовлено тим, що додавання проводиться за модулем 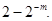
Загальні правила додавання двійкових операндів, представлених у формі з фіксованою комою (правильні дроби), в оберненому коді можна розглянути на підставі застосування доповнення до двох і доповнення до одиниці (див. розділ 3). Розгляд будемо вести для двох основних варіантів:
а) 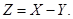
Обчислимо цей вираз із застосуванням доповнень.
Як відомо, для правильних двійкових дробів
|
|
Тоді
|
|
де 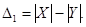
Розглянемо такі три випадки:
1) Якщо 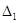 < 0, то
< 0, то 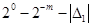 <
< 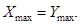
Це означає, що не виникає перенесення до знакового розряду, а, також, із знакового розряду в молодший розряд результату (циклічного перенесення).
Результат операції є від'ємний і записується в оберненому коді так:
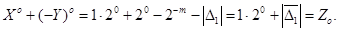 4.
4.
2) Якщо 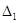 > 0, то
> 0, то 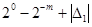 >
> 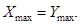
Це означає, що виникає перенесення до знакового розряду, а, також, із знакового розряду в молодший розряд результату. Додаючи перенесення із знакового розряду до отриманого результату з вагою 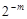 , отримаємо додатній результат, який записується в оберненому коді так:
, отримаємо додатній результат, який записується в оберненому коді так:
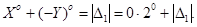
3) Якщо 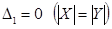 , то отримаємо результат:
, то отримаємо результат:
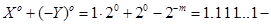 один із варіантів визначення нуля в оберненому коді.
один із варіантів визначення нуля в оберненому коді.
б)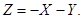
Обчислимо в оберненому коді:
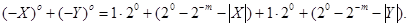
Вираз
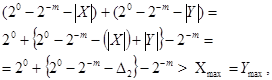
де 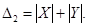
Це означає, що виникає перенесення до знакового розряду, а, також, із знакового розряду. Додаючи перенесення із знакового розряду до отриманого результату з вагою 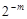 , отримаємо правильний від'ємний результат, який записується в оберненому коді так:
, отримаємо правильний від'ємний результат, який записується в оберненому коді так:
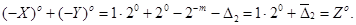
Отримані результати дають право зформулювати таке правило додавання двох чисел в оберненому коді:
Сума двох чисел в оберненому коді дорівнює сумі їх обернених кодів з урахуванням знакових розрядів. У випадку виникнення перенесення із знакового розряду одиниця перенесення додається до результату, як одиниця молодшого розряду.
Наступні приклади ілюструють чотири основні варіанти додавання чисел у оберненому коді при виконанні умови 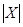 >
> 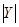 і
і 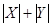 < 1.
< 1.
1) 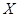 > 0;
> 0; 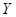 > 0;
> 0; 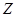 > 0;
> 0;
Приклад 1.
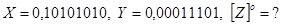

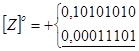 .
.
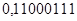
У звязку з тим, що обернений код додатніх чисел співпадє з записом самих чисел, оприманий результат співпадає з результатом додавання цих чисел у прямому коді.
2) 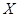 > 0;
> 0; 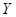 < 0;
< 0; 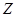 > 0;
> 0;
Приклад 2.
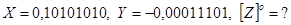

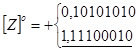
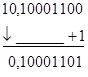
Виникає перенесення в знаковий розряд і із знакового розряду. Необхідно провести корекцію результату.
3) 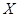 < 0;
< 0; 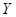 > 0;
> 0; 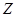 < 0;
< 0;
Приклад 3.
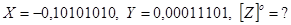

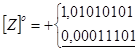
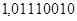
Сума від'ємна. Перенесення до знакового розряду немає. Корекція не потрібна.
4)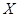 < 0;
< 0; 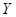 < 0;
< 0; 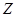 < 0;
< 0;
Приклад 4.
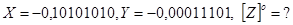

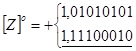
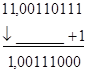
Сума від'ємна. Виникає перенесення в знаковий розряд і із знакового розряду. Необхідно провести корекцію результату.
Очевидно, що у всіх розглянутих випадках додавання операнди можна поміняти місцями, і при цьому результат не зміниться.
Таким чином, обернений код досить зручний для виконання операцій алгебраїчного додавання, якщо врахувати простоту переведення від'ємних чисел із прямого кода в обернений і навпаки.