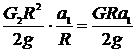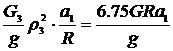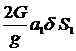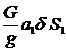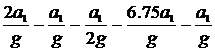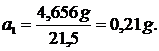4.1 Приклад виконання завдання

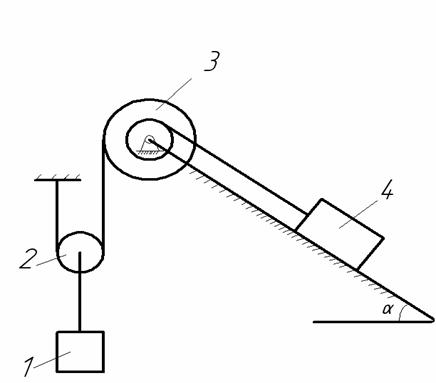
Дано: G₁ = 2G; G₂ = G; G₃ = 3G; G₄ = G; R₂ = R; R₃ = 2R; r₃ = R;

f = 0.2; r₃ =1.5 R; a = 30° (рис. АМ4.6).

       Визначити прискорення вантажу 1 i натяг Т_1-2, Т_3-4, Т_2-3.

 Рисунок АМ4.6

Для розв'язання задачі використаємо загальне рівняння динаміки. Покажемо задані сили: сили ваги G₁ - вантажу 1, G₂ - блока 2, G₃ - блока 3 i G₄ - вантажу 4, а також силу тертя ковзання F - вантажу по похилій площині (рис. АМ4.7).

 Прикладемо  сили   інерції.   Сила інерції вантажу 1,  який  рухається поступально з прискоренням а₁, виражається вектором

Сила інерції блока 2, який рухається плоско-паралельно, зводиться до вектора

де  - прискорення центра ваги блока, i пари сил, момент якої 

    Сила інерції вантажу 4, який рухається поступально з прискоренням , виражається вектором           .

      Надаємо системі можливе переміщення (рис. АМ4.7) i складемо загальне рівняння    динаміки:

Рисунок АМ4.7

G₁S₁ + G₂S₂ – G₄ sinS₄ – FS₄ – Ф₁S₁ –

                      – Ф₂S₂ – М – М – Ф₄S₄ =0                       (4.1)

      Згідно з умовою задачі розтягом нитки нехтуємо, тоді прискорення центра мас вантажу 1, блока 2 та кутове прискорення блока 2  і 3 такі :

₂ = _1,                                                                                        (4.2)

= /R , = 2/R₃ = /R ,

де ₁  -     прискорення вантажу 1 .

        Кутове прискорення нерухомого блока 3 :

                                                        = 2₁/R₃                                                                                        (4.3)

      Прискорення вантажу 4:      ₄ = ∙ r₃ =                                   (4.4)

      Тоді з врахуванням (4.2)-(4.4) запишемо вирази для сил інерції  Ф₁  і  Ф₂ та  моментів сил інерції     М і  М :                                  

                                           ,                                                        (4.5)

                                           Ф₂ = m₂₂ = = ,                                       (4.6)

                                           Ф₄ = m₄= ,                                                      (4.7)

                                           М= І_{2 х} = ,                              (4.8)

  М=І_3х =.                        (4.9)

       де І_2х =  - момент інерції однорідного блока 2 відносно централь- ної осі Х;

       І_{3 х} =  - момент інерції східчастого шківа 3.

        Сила тертя ковзання вантажу 4 :

                                          F = f G₄ cos = f G cos.                                  (4.10)

        Виразимо переміщення S₂, S₄, ₂, ₄      через S_l.

                                                  S₂ = S₁ ,  ₂ = S₂/R=S₁/R  ,                        (4.11)

₃ = =

= = = .

       Рівняння (4.1) має вигляд:

2GS₁ + GS₁ – G sinS₁ – f G cos S₁– – –

      – ––=0.                                          (4.12)

       Після ділення отриманого рівняння на  GS₁ отримаємо :

3 – 0,5 – 0,2∙0,86 –   = 0,

2,328 –  = 0.

Звідки                                                  

 Для визначення натягу нитки в дільницях 1-2, 2-3, 3-4 ( рис. АМ4.6) умовно розріжемо її і замінимо відповідно реакціями T_1-2 ,  T_2-3 , T_3-4  .

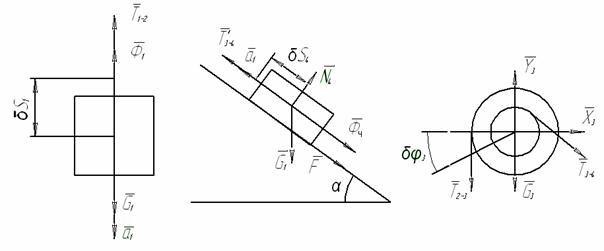
      Рисунок АМ4.8                  Рисунок АМ4.9                  Рисунок АМ4.10

      Показавши на кожному рисунку сили інерції з врахуванням відповідних переміщень кожної частини даної механічної системи, складаємо загальні рівняння динаміки.

       Для рис. АМ4.8 :

                                           G₁dS₁ – Ф₁dS₁ – T_1-2dS₁ = 0.                                     (4.13)

        Підставивши значення сили інерції Ф₁  в (4.13), та скоротивши отримане рівняння на dS₁, знаходимо натяг нитки на дільниці 1-2:

      T_1-2 = G₁ – Ф₁ = 2G – a₁ = 2G – =1,57G.

         Для рис. АМ4.9 :

                                   T_3-4 dS₄ – G sin dS₄ – G f cos dS₄ –Ф₄ dS₄ = 0.         (4.14)

Підставивши значення сили інерції Ф₄  в (4.14), та скоротивши отримане рівняння на dS₄, знаходимо натяг нитки на дільниці 3-4:

            T_3-4 = G sin + G f cos + a₁ =G (0,5 + 0,2 ∙0,86 + ) = 0,89G.

         Для рис. 4.10 :

                                                  T_2-3∙2S₁ – T_3-4∙S₄ = 0,                                (4.15)

           Враховуючи, що і S₄ = S₁, отримаємо:      

 (T_2-3∙2 – T_3-4)S₁ = 0,

   Скорочуючи отримане рівняння на S₁, знаходимо значення натягу  нитки на дільниці 2-3:

T_2-3 = T_3-4/2 = 0,55G.