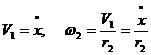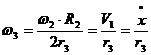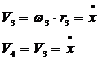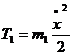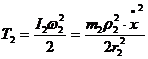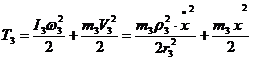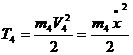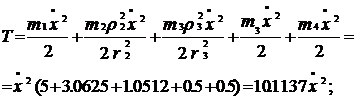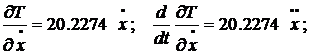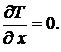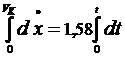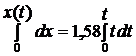5.1 Приклад виконання завдання

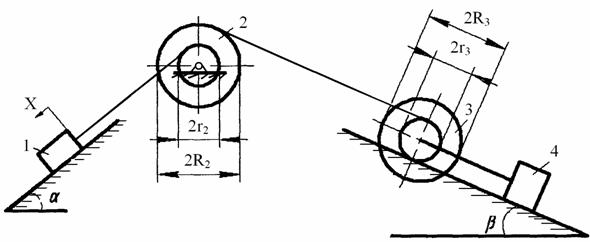
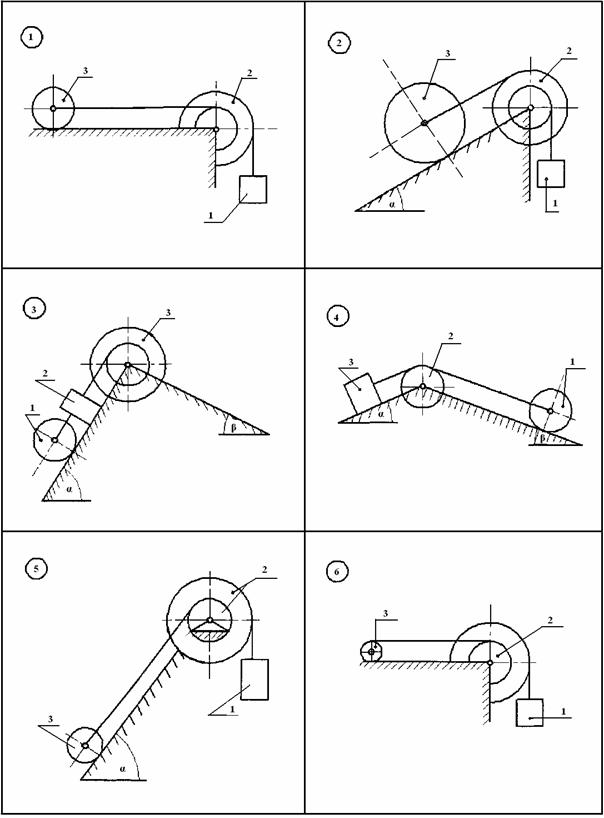
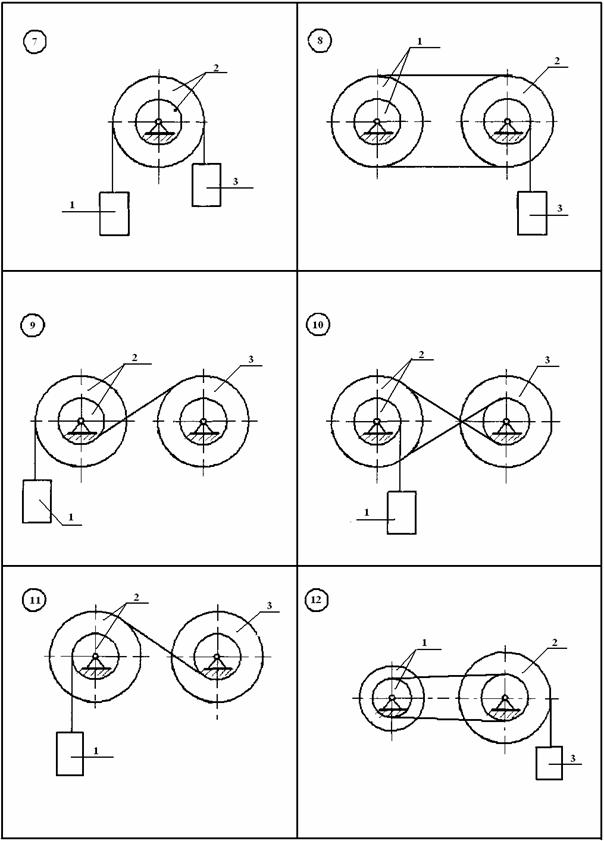
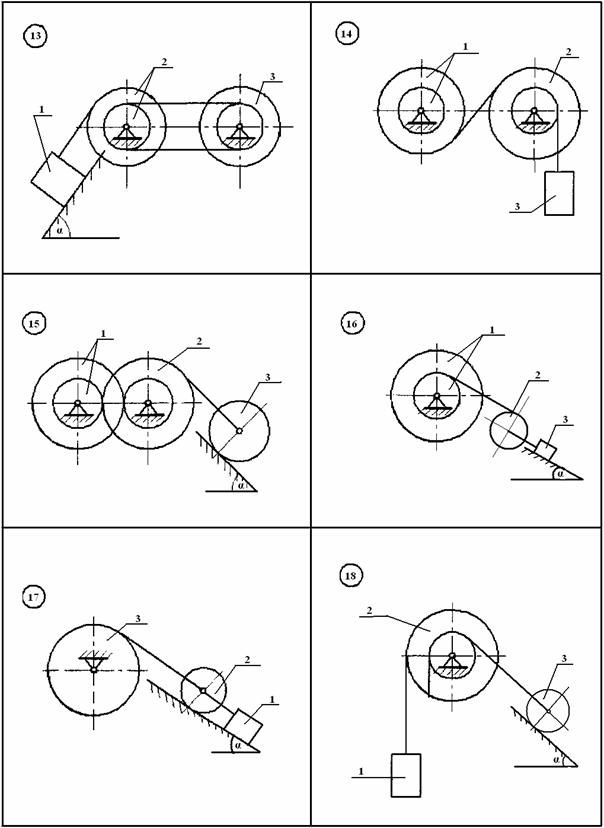
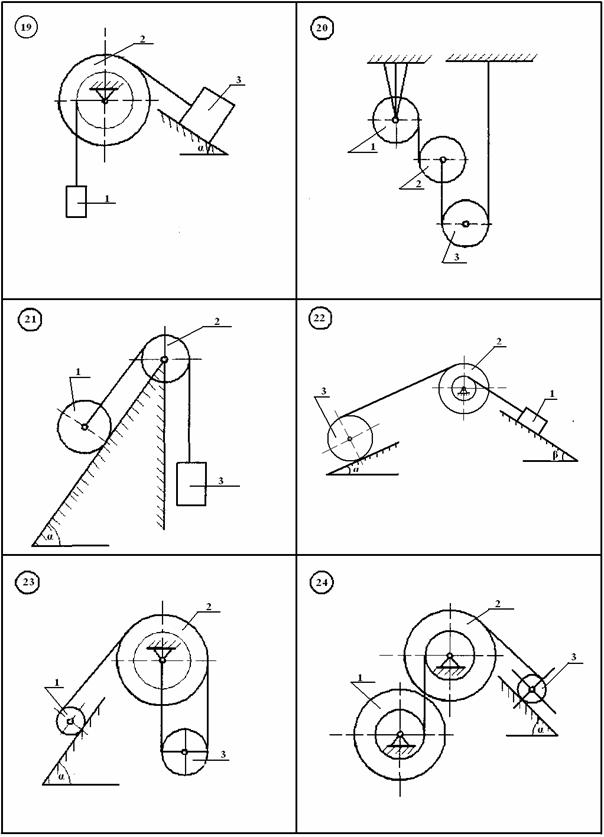
Визначити прискорення та закон руху центра мас тіла 1, якщо матеріальна система (рис.АМ5.1 ) починає рухатися із стану спокою, масами шнурів знехтувати. Тіла 1 та 3 рухаються без ковзання.     

Дано:  

;º; º.

Початкові умови: q₁₀ = 0; .

Рисунок АМ5.1

Розв’язання. За узагальнену координату виберемо переміщення  тіла 1 вздовж похилої площини. Для розв’язання задачі використаємо рівняння Лагранжа другого роду

                                              ,                                         (5.1)

де Т - кінетична енергія системи;

          Q - узагальнена сила.

Визначаємо швидкості центрів мас та нульові швидкості твердих тіл системи через узагальнену швидкість :

- кутова швидкість блока 2,

- кутова швидкість блока 3.

Моменти інерції блоків відносно центральних осей:

.

Кінетична енергія тіл 1-4:

- поступальний рух тіла 1;

- обертальний рух блока 2;

- блок 3 звершує плоско-паралельний рух

 -  поступальний рух тіла 4.

Для даної системи

                        ;    (5.2)

 Підставимо знайдені кінетичні енергії в формулу (5.2), маємо:

                         (5.3)

Тоді

                                                                                                  (5.4)

Знайдемо узагальнену силу Q за формулою:

                                              .                                             (5.5)

Для знаходження елементарної роботи  спочатку визначаємо роботу сил, діючих на механічну систему з врахуванням переміщення  х.

                    .

                    ;

- центр мас блока 2 не переміщується.

Оскільки , то , тоді

                    .

                    .

Отже, робота зовнішніх сил, які діють на механічну систему, має вигляд:

                                                    (5.6)

Звідки      .                            (5.7)

Підставимо (5.7) в формулу (5.5):

       (5.8)

           Тоді з врахуванням (5.4) і (5.8) рівняння Лагранжа (5.1) запишеться у вигляді:

                                                                                            (5.9)

Звідки знаходимо прискорення тіла 1:

                                                .                                                 (5.10)

Проінтегруємо двічі рівняння (5.9) з врахуванням початкових умов.

,

,

,

,

.

Рисунок АМ5.11

Рисунок АМ5.12

Рисунок АМ5.13

Рисунок АМ5.14

 Рисунок АМ5.15