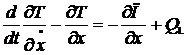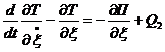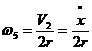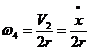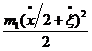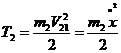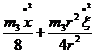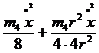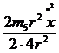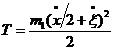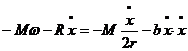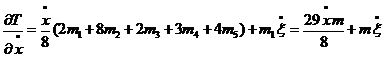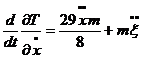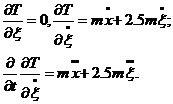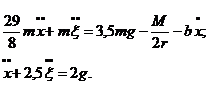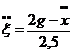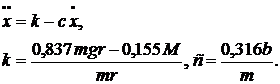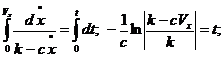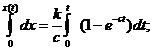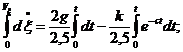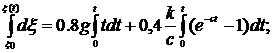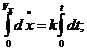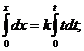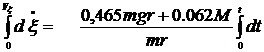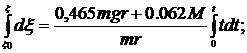|
|
||
|
|
6.1 Приклад виконання завдання
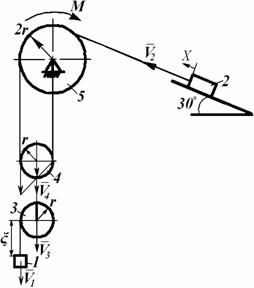
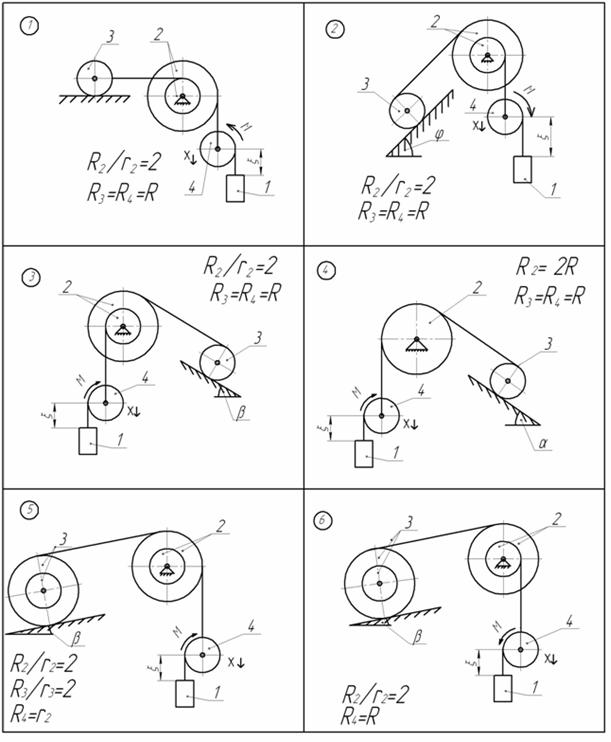
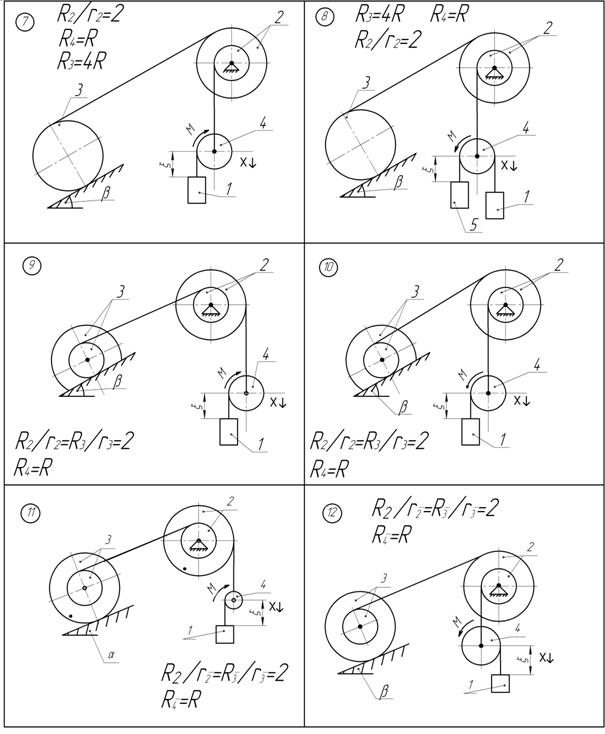
Дано: маси тіл механічної системи (рис. АМ6.1): m1=2m; m2=m; m3=m; m4=m; m5=3m; М - постійний момент, який прикладений до колеса 5;
де b - коефіцієнт пропорційності;
Всі колеса вважаються однорідними суцільними дисками.
Знайти рівняння руху
системи в узагальнених координатах
q1= x ; q2=
Початкові умови:
Розв’язання. Для розв’язання задачі використаємо рівняння Лагранжа другого роду:
де Т- кінетична енергія системи; П - потенціальна енергія;
Q1
і Q2 – узагальнені сили, які відповідні
узагальненим координатам х і
Рисунок АМ6.1 Виразимо швидкості центрів мас твердих тіл системи через узагальнені швидкості:
Блок 4 звершує
плоско-паралельний рух (миттєвий центр швидкостей - точка Р4),
тому швидкість центра мас блока буде вдвічі менша ніж швидкість
Тягарець 1
звершує складний рух, де V3 – переносна
швидкість,
Визначимо кутові швидкості тіл 5, 4 і 3:
Моменти інерції коліс відносно центральних осей:
Кінетична енергія тіл 1-5:
Для даної системи
Підставимо знайдені кінетичні енергії тіл в (6.3), маємо:
=
Потенціальну
енергію системи знаходимо як роботу сил ваги твердих тіл 1, 3, 4, 2
при їх переміщенні з даного положення, що характеризується
координатами х і
П=П1+П2+П3+П4; (6.5)
П1=-m1g(x+
П3=-m3
g y3 =-m3 g
Оскільки
швидкість центр мас тіла V3=
Аналогічно розмірковуючи, маємо
П4=-m4
g y4 =-m4 g
Підставляючи отримані значення в (6.5), маємо:
П=-m1
g(x+
=-2mg(x+
Тоді
Узагальнені сили Q1 і Q2 можна визначити з виразу роботи неконсервативних сил на елементарних переміщеннях системи, які відповідають варіації кожної узагальненої координати, або з виразів потужностей N1 і N2 неконсервативних сил на можливих швидкостях системи, які відповідають зростанню кожної узагальненої координати.
Оскільки до блока 5
прикладено постійний момент М , а до тіла 2 сила в’язкого
опору
R=b
де N1-
потужність пари сил М з врахуванням швидкості
В результаті маємо:
Узагальнена сила Q2 = 0, оскільки неконсервативних сил на елементарному переміщенні dξ немає. Тепер за рахунок (6.4) запишемо складові лівих частин (6.1) і (6.2):
З врахуванням (6.6) - (6.8) рівняння (6.1) - (6.2) запишуться у вигляді:
Для розв’язання рівнянь (6.9)
виразимо
Підставимо (6.10) в перше рівняння (6.9), маємо:
де
Проінтегруємо двічі (6.11) з
врахуванням початкових умов
Отже рівняння (6.12) характеризує переносний рух тіла 1,
Підставимо
Проінтегруємо
двічі (6.13) з врахуванням початкових умов:
Отже, (6.12), (6.14) є рівняннями руху даної механічної системи.
Примітка. Якщо відсутня сила в’язкого опору, то
Q1=-M/2r.
Тоді рівняння (6.11) запишеться у вигляді
Інтегруючи (6.15) з врахуванням початкових умов, маємо:
VX= kt,
або
Підставимо з (6.15) вираз
Проінтегруємо двічі рівняння (6.17) з врахуванням початкових умов
Рисунок АМ6.2
Рисунок АМ6.3
Рисунок АМ6.4
Рисунок АМ6.5
Рисунок АМ6.6
|
|