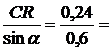3.1 Приклад виконання завдання

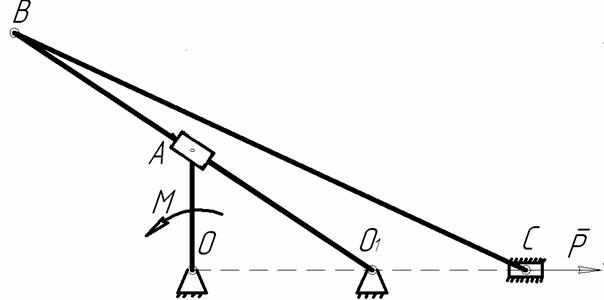
Дано: М= 6 Нм ;  ОА= 0,15 м;  ОО₁=0,2 м ; О₁В=0,5м ; ВС = 0,78 м

(рис. АМ3.6). Нехтуючи тертям, визначити  величину Р, яку необхідно прикласти до повзуна С, щоб механізм знаходився в рівновазі, коли ОАОО₁.

Рисунок АМ3.6

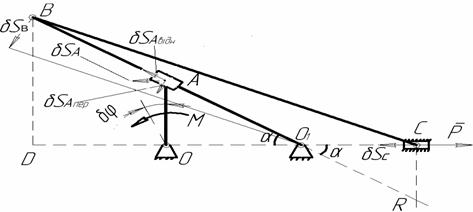
Розв’язання. Конструкція знаходиться в рівновазі під дією пари сил М і сили Р. В’язі, які діють на неї, допускають переміщення повзуна С на  δSС, кривошипа ОА – на δφ.

Знайдемо залежність між можливими переміщеннями точок системи. За рахунок шарнірного з’єднання з кривошипом ОА трубка (точка) А переміщується на δSА_ - абсолютне переміщення, одночасно переміщується по стержню ВО1 на δSАвідн. - відносне переміщення і зі стержнем ВО1 на   δSАпер. - відносне переміщення (рис. АМ3.7).

 Рисунок АМ3.7

Визначимо можливе переміщення δSС через переміщення кривошипа δφ. Для цього необхідно знайти переміщення вузла (точки) В – δSВ шатуна ВС. На рис. АМ3.7 позначимо кут ОО1В через a. Оскільки точка В теж належить коромислу ВО1, то знайдемо залежність δSВ через δSA пер.

δSAпер   QUOTE  = δSA·sin α, де δSA= δj·OA, sinα =   QUOTE  .

Відстань AO1=(м).

Оскільки О1В= 50 см = 0,5 м , а АО1 = 0,25 м , то переміщення

           δSВ= 2 δSAпер = 2δSAsinα = QUOTE  δSA ,  де sinα =  QUOTE   =  QUOTE  .

Для визначення залежності між можливими переміщеннями δS_В і δS_С знайдемо положення миттєвого центра обертання ланки ВС – точка R.

Тоді                       QUOTE   = QUOTE    ,     звідки         δS_С =  QUOTE   .

          Визначаємо ВR  і  CR . Для цього розглянемо трикутники DBO₁ , DBC₁ і DRO_{1 .}

З ∆DBO₁ ð BD = 2 АО= 0,3 м.

З ∆DBС ð DC =  QUOTE   =  QUOTE   = 0,72 (м).

Тоді О₁С = DC – DO₁ = 0,72 – 0,4 = 0,32 (м).

З ∆ СO₁R  ð CR = O₁C· tga = 0,32· QUOTE  = 0,24 м, де tga =  QUOTE   = =  QUOTE  .

О₁R =  QUOTE  0,4 м, ВР = О₁Р + О₁R = 0,5+0,4 = 0,9 (м).

Тоді δS_С  = 1,2 δS_A  QUOTE   = 0,32 δS_A = 0,32·0,15 = 0,048 δφ.

       Рівняння робіт, яке виражає принцип можливих переміщень,  має вигляд:

                                            М δφ – Р δS_С = 0,                                                (3.1)

 або     6 ·δφ –  0,048·Р ·δφ = 0.    Звідки    Р =  QUOTE   = 125 (Н).

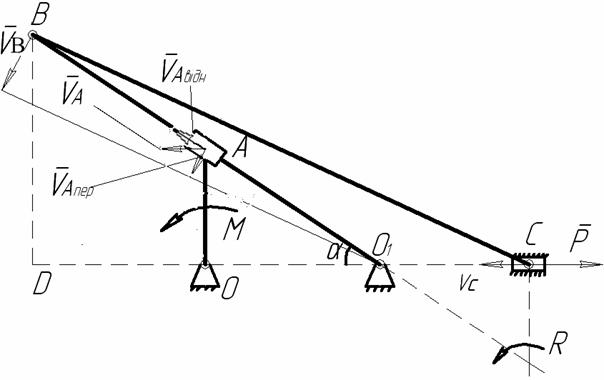
       Розглянемо розв'язання задачі з врахуванням того, що сума потужностей сил, які діють на механічну систему у випадку рівноваги дорівнює нулю.

       Надаємо кривошипу ОА можливу кутову швидкість w (рис. АМ3.8) . Тоді вузлові точки А, В і С ланок механізму набувають відповідно швидкість V_A, V_B і V_C. На рис. АМ3.8 покажемо напрям швидкостей вузлових точок механізму, застосовуючи поняття миттєвого центра швидкостей для кожної його ланки (точка А-миттєвий центр швидкостей (МЦШ) для ланки ОА, О₁ – МЦШ для ланки О₁В, R-  МЦШ для ланки ВС).  

       Запишимо рівняння потужностей:   Mω- РV_c = 0.                               (3.2)

       Оскільки повзун А звершує складний рух , то абсолютна швидкість V_A дорівнює сумі переносної швидкості V_А^пер і відносної швидкості V_А^відн (рис. АМ3.8).

Рисунок АМ3.8

З попередніх розрахунків маємо: sina =, . Отже, відстань точки B до центра обертання  вдвічі більша, тоді

          Для визначення кутової швидкості ланки знайдемо відстань , де - миттєвий центр швидкостей ланки .

      В результаті маємо, що кутова швидкість ланки

      Тоді швидкість точки С

V_c =ω QUOTE  _R ·CR =  QUOTE   · 0,24 = 0,32 · V_A.

           _{Кутова швидкість кривошипа ОА :}

 _QUOTE  ω _{= =}

       Підставимо  значення  ω і V_C в формулу ( 3.2), маємо:

М · =0,32·P·V_A .

       Звідки  Р = 125 (Н).