2 ПЛОСКА СИСТЕМА СИЛ

2.1 Теоретичні відомості і методичні вказівки

У теоретичній механіці одним із основних є поняття сили. У механіці під силою розуміють  міру механічної взаємодії матеріальних тіл, у результаті якої тіла, що взаємодіють, можуть надавати одне одному прискорення або деформуватися (змінювати свою форму). Із цього означення випливають два методи вимірювання сили:

1. Динамічний, в основі якого лежить вимірювання прискорення тіла в інерціальній системі відліку;

2. Статичний, побудований на вимірюванні деформації пружних тіл.

Те, що в основу механіки було покладено кількісні закони сил, дозволило  І. Ньютону відкрити закони руху тіл, не вивчаючи фізичних явищ, які виникають при взаємодії тіл. Більш того, в деяких випадках можна встановити кількісний зв’язок між механічними і немеханічними формами матерії при їх взаємних перетвореннях.

Модель сили   визначається трьома головними умовами: величиною, напрямом дії і точкою прикладення.

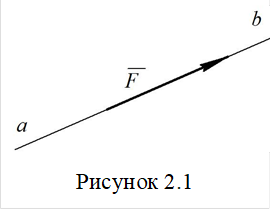Такому означенню сили повністю відповідає поняття вектора, довжина якого у вибраному масштабі дорівнює величині (модуля) сили, прикладеної в даній точці. Вектор напрямлений в бік дії сили. Силу позначимо символом  (рис. 2.1).

Пряму , на якій відкладено відрізок, що зображує силу, називають лінією дії сили.

Для вимірювання модуля сили її порівнюють з іншою силою, яку вважають еталоном. У системі СІ за одиницю сили (еталон) прийнято Ньютон (). Використовуються також більші одиниці вимірювання сил: кілоньютон (); меганьютон ().

Сила, як векторна величина, підпорядкована всім законам векторного числення: додавання; віднімання; векторного та скалярного множення.

Алгебраїчним моментом сили відносно точки називається взятий з відповідним знаком добуток плеча на модуль сили. Знак “+” береться, якщо сила намагається повернути плече проти напрямку стрілки годинника.

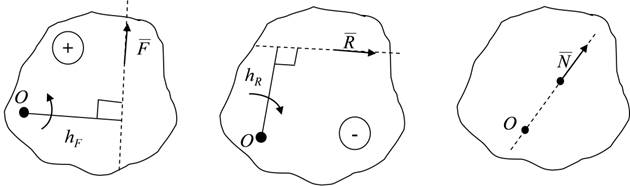
Таким чином, для визначення алгебраїчного моменту сили відносно точки треба виконати такі дії (рис. 2.2,а,б):

1. провести лінію дії сили;

2. з вибраної точки опустити перпендикуляр до лінії дії сили (довжина перпендикуляра h – плече сили);

3. знайти добуток плеча h на модуль сили;

4. момент сили буде додатним, якщо сила намагається повернути плече відносно вибраної точки проти напрямку стрілки годинника (рис. 2.2, а) і знак “–“ – за напрямком стрілки годинника (рис. 2.2, б).

Рисунок 2.2

Окремий випадок (рис. 2.2, в): алгебраїчний момент сили відносно точки дорівнює нулю, якщо лінія дії сили проходить через цю точку (тут плече h=0).

Умови рівноваги довільної плоскої системи сил в аналітичній формі.

      Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчні суми проекцій сил на дві взаємно перпендикулярні осі і алгебраїчна сума моментів відносно довільно вибраної точки дорівнювали нулю.

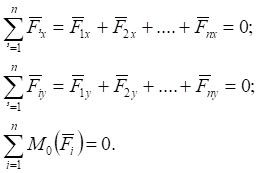
Питання для самоперевірки знань

та контролю засвоєння матеріалу

1.Яка величина є основним поняттям в механіці?

2. Знайти суму (різницю) двох сил.

3. Знайти векторний (скалярний) добуток двох сил.

4.Методика визначення моменту сили відносно точки.

5. Умови рівноваги плоскої довільно розташованої системи сил.