4.2 Методи аналізу великих систем, факторний аналіз
Даний параграф є заключним і в ньому розглянута ще одна особливість методів системного аналізу, показано ще один шлях до досягнення професійного рівня в області керування системами.
Вже зрозуміло, що ТССА здебільшого засновує свої практичні методи на основі математичної статистики. Загальновизнано, що в наші дні можна виділити три підходи до розв’язання задач, у яких використовуються статистичні дані.
- Алгоритмічний підхід, за яким ми маємо статистичні дані про деякий процес і через слабку вивченість процесу ми змушені самі будувати «розумні» правила обробки даних, базуючись на своїх власних уявленнях про показник, що нас цікавить.
- Аппроксимаційний підхід, коли ми повністю розуміємо, який існує зв’язок даного показника з наявними у нас даними, але незрозуміла природа виникаючих помилок – відхилень від цих представлень.
- Теоретико-вірогідний підхід, коли потрібно глибоко розуміти суть процесу для з’ясування зв’язку показника із статистичними даними.
На даний час усі ці підходи досить строго науково обґрунтовані і містять апробовані методи практичних дій. Однак існують ситуації, коли нас цікавить не один, а кілька показників процесу і, крім того, ми підозрюємо наявність декількох впливаючих на процес факторів, які є прихованими, латентними, або їх не можна спостерігати.
Найцікавішим і корисним у плані розуміння сутності факторного аналізу – методу розв’язання задач у цих ситуаціях, є приклад використання спостережень експерименту, який проводить природа, ні про яке планування тут не йдеться – ми повинні задовольнятися пасивним експериментом.
Дивно, але й у цих «важких» умовах ТССА пропонує методи виявлення таких факторів як відсівання слабко виявляючих себе, оцінки значимості отриманих залежностей показників роботи системи від цих факторів.
Нехай ми провели по n спостережень за кожним з k вимірюваних показників ефективності деякої системи і дані цих спостережень представили у вигляді матриці вхідних даних E[n×k] (табл. 4.5).
| E11 | E12 | ... | E1i | ... | E1k |
| E21 | E22 | ... | E2i | ... | E2k |
| ... | ... | ... | ... | ... | ... |
| Ej1 | Ej2 | ... | Eji | ... | Ejk |
| ... | ... | ... | ... | ... | ... |
| En1 | En2 | ... | Eni | ... | Enk |
Нехай ми припускаємо, що на ефективність системи впливають і інші величини (фактори), які не спостерігаються, але їх можна легко інтерпретувати (з’ясувати зміст, причини і механізми впливу). Відразу ж зрозуміємо, що чим більше значення n і чим менше число факторів m (а може їх і немає взагалі), тим більша можливість оцінити їх показник E, що нас цікавить. Настільки ж легко зрозуміти і необхідність умови m < k, з’ясованої на простому прикладі аналогії – якщо ми досліджуємо деякі предмети з використанням усіх 5 людських почуттів, то наївно сподіватися на виявлення більше п’яти «нових» ознак у придметах, які можна легко пояснити, але не можна виміряти, навіть якщо ми «випробуємо» дуже велику їх кількість.
Повернемося до вихідної матриці спостережень E[n × k] і відзначимо, що перед нами, у дійсності, сукупності по n спостережень над кожною з k випадковими величинами E1, E2, … Ek. Саме ці величини «підозрюються» у зв’язках одна з іншою – або у взаємній корельованості.
З розглянутого раніше методу оцінок таких зв’язків випливає, що мірою розкиду випадкової величини Ei є її дисперсія, що обумовлена сумою квадратів усіх зареєстрованих значень цієї величини Σ(Eij)2 і її середнім значенням (додавання ведеться за стовпцями).
Якщо ми застосуємо заміну змінних у вихідній матриці спостережень, тобто замість Eij будемо використовувати випадкові величини
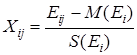 ,(4.2)
,(4.2)
то ми перетворимо вихідну матрицю у нову матрицю X [n × k] (табл. 4.6).
| X11 | X12 | ... | X1i | ... | X1k |
| X21 | X22 | ... | X2i | ... | X2k |
| ... | ... | ... | ... | ... | ... |
| Xj1 | Xj2 | ... | Xji | ... | Xjk |
| ... | ... | ... | ... | ... | ... |
| Xn1 | Xn2 | ... | Xni | ... | Xnk |
Відзначимо, що всі елементи нової матриці X [n × k] є безрозмірними, нормованими величинами і, якщо деяке значення Xij складе, приміром, +2, то це буде означати тільки одне – у рядку j спостерігається відхилення від середнього по стовпцю i на два середньо-квадратичних відхилення (у більшу сторону).
Виконаємо тепер такі операції.
- Підсумуємо квадрати всіх значень стовпця 1 і розділимо результат на (n – 1) – ми одержимо дисперсію (міру розкиду) випадкової величини X1, тобто D1. Повторюючи цю операцію, ми знайдемо такий же самим чином дисперсії всіх величин, які спостерігаються, але вже є нормованими величинами.
- Підсумуємо добуток відповідних рядків (від j = 1 до j = n) для стовпців 1, 2 і також розділимо на (n – 1). Те, що ми отримали, називається коваріацією C12 випадкових величин X1, X2 і служить мірою їх статистичного зв’язку.
- Якщо ми повторимо попередню процедуру для всіх пар стовпців, то у результаті отримаємо ще одну, квадратну матрицю C[k×k], яку називають коваріаційною. На її головній діагоналі стоять дисперсії ВВ величин Xi, а інші її елементи – коваріації цих величин (i = 1..k) (табл. 4.7).
| D1 | C12 | C13 | ... | ... | C1k |
| C21 | D2 | C23 | ... | ... | C2k |
| ... | ... | ... | ... | ... | ... |
| Cj1 | Cj2 | ... | Cji | ... | Cjk |
| ... | ... | ... | ... | ... | ... |
| Cn1 | Cn2 | ... | Cni | ... | Dk |
Якщо згадати, що зв’язок ВВ можна описувати не тільки коваріаціями, але й коефіцієнтами кореляції, то у відповідність цій матриці можна поставити матрицю парних коефіцієнтів або кореляційну матрицю R [k×k] з одничною діагоналлю, а всі її інші елементи – коефіцієнти парної кореляції (табл. 4.8).
| 1 | R12 | R13 | ... | ... | R1k |
| R21 | 1 | R23 | ... | ... | R2k |
| ... | ... | ... | ... | ... | ... |
| Rj1 | Rj2 | ... | Rji | ... | Rjk |
| ... | ... | ... | ... | ... | ... |
| Rn1 | Rn2 | ... | Rni | ... | 1 |
Отже, нехай ми думали, що змінні E, за якими ми спостерігали, є незалежними одна від одної, тобто ми очікували побачити матрицю R [k×k] діагональною, з одиницями на головній діагоналі і нулями в інших місцях. Якщо тепер це не так, то наші здогади про наявність латентних факторів дещо отримали підтвердження.
Але ж як переконатися в правильності наших міркувань, оцінити достовірність нашої гіпотези – про наявність хоча б одного латентного фактора, як оцінити степінь його впливу на основні (ті що спостерігаються) змінні? А якщо, тим більше, таких факторів лише декілька – то як їх проранжувати за степенем впливу?
Відповіді на такі практичні питання повинен давати факторний аналіз. У його основу покладено метод статистичного моделювання (за висловлюванням В. В. Налімова – модель замість теорії).
Подальший хід аналізу при з’ясуванні таких питань залежить від того, якою з матриць ми будемо користуватися. Якщо матрицею коваріацій C [k×k], то ми маємо справу з методом головних компонентів, якщо ж ми будемо користуватися лише матрицею R [k×k], то ми використовуємо метод факторного аналізу у його звичайному вигляді.
Залишається з’ясувати, що дозволяють обидва ці методи, у чому полягає їх відмінність і як ними користуватися. Призначення обох методів однакове – встановити факт наявності латентних змінних (факторів), і якщо вони виявлені, то отримати кількісний опис їх впливу на основні змінні Ei.
Хід міркувань при виконанні пошуку головних компонентів полягає у такому. Ми припускаємо наявність некорельованих змінних Zj (j = 1...k), кожна з яких описана комбінацією основних змінних (додавання по i = 1...k):
Zj = ∑Aji×Xi,(4.3)
і, крім того, має дисперсію, таку що
D(Z1) ≥ D(Z2) ≥ D(Zk).(4.4)
Пошук коефіцієнтів Aji (їх називають вагою j-ого компонету в змісті i-ої змінної) зводиться до розв’язання матричних рівнянь і не являє особливої складності при використанні комп’ютерних програм. Але сутність цього методу дуже цікава і на ній варто зупинитися.
Як відомо з векторної алгебри, діагональна матриця [2×2] може розгляддатися як опис 2-х точок (точніше – вектора) у двовимірному просторі, а така ж матриця розмірністю [k×k] – як опис k точок k-мірного простору. Отож, заміна реальних, хоча і нормованих змінних Xi на точно таку ж кількість змінних Zj означає не що інше, як поворот k осей багатомірного простору.
«Перебираючи» по черзі осі, ми знаходимо спочатку ту з них, де дисперсія вздовж осі найбільша. Потім робимо перерахування дисперсій для k – 1 осей, що залишилися і знову знаходимо «вісь-чемпіона» по дисперсії і т.д.
Тобто, ми розлядаємо куб (3-х мірний простір) по черзі по трьох осях і спочатку шукаємо той напрямок, де бачимо найбільший «туман» (найбільша дисперсія говорить про найбільший вплив чогось стороннього); потім «усереднюємо» картинку по двох осях, що залишилися, і порівнюємо розкид даних по кожній з них – знаходимо «середнячка» і «аутсайдера». Тепер залишається розв’язатити систему рівнянь – у нашому прикладі для 9 змінних, щоб відшукати матрицю коефіцієнтів (ваг) A [k×k].
Якщо коефіцієнти Aji знайдено, то можна повернутися до основних змінних, оскільки доведено, що вони однозначно відображаються у вигляді (додавання по j = 1...k):
Xi = SAji×Zj,(4.5)
Пошук матриці ваг A [k×k] вимагає використання коваріаційної матриці і кореляційної матриці. Таким чином, метод головних компонентів відрізняється від усіх інших тим, що дає завжди єдиний розв’язок задачі. Правда, трактування цього розв’язку своєрідне:
– ми розв’язуємо задачу про наявність відповідно стількох факторів, скільки в нас спостерігається змінних, тобто питання про нашу згоду на менше число латентних факторів неможливо поставити;
– у результаті розв’язок, теоретично, завжди єдиний, а практично зв’язаний з великими обчислювальними труднощями при різних фізичних розмірностях основних величин. Ми отримаємо відповідь приблизно такого вигляду – фактор такий-то (наприклад, привабливість продавців під час аналізу денного виторгу магазинів) займає третє місце по степеню впливу на основні змінні.
Ця відповідь обумовлена тим, що дисперсія цього фактору виявилася третьою по величині серед усіх інших. Більше нічого отримати у цьому випадку не можливо. Інша справа, або цей висновок виявився нам корисним, або ми його проігноруємо – це наше право вирішувати, як використовувати системний підхід!
Трохи інакше здійснюється дослідження латентних змінних у випадку застосування факторного аналізу. Тут кожна реальна змінна розгляддається як лінійна комбінація ряду факторів Fj, але у трохи незвичайній формі
Xi = SBji×Fj+Di,(4.6)
причому додавання ведеться по j = 1...m, по кожному факторові.
Тут коефіцієнт Bji прийнято називати навантаженням на j-й фактор з боку i-ї змінної, а останній доданок у (4.6) розглядається як перешкода – випадкове відхилення для Xi. >Число факторів m цілком може бути менше від числа реальних змінних n і ситуації, коли ми хочемо оцінити вплив лише одного фактора (ввічливість продавців), тут цілком допустимі.
Саме поняття «латентний», схований, є фактором, який не можна виміряти безпосередньо. Звичайно ж, немає приладу і немає еталона ввічливості, освіченості, витривалості і т.п. Але це не заважає нам самим «виміряти» їх, застосувавши відповідну шкалу для таких ознак, розробивши тести для оцінки таких властивостей по цій шкалі, і застосувавши ці тести до тих же продавців. Так у чому ж тоді «неспостережність»? А у тому, що в процесі експерименту (обов’язково) масового ми не можемо безупинно порівнювати всі ці ознаки з еталонами і нам потрібно брати попередні, усереднені дані, які отримані зовсім не в «робочих» умовах.
Розглянемо ще й такий приклад. Хто буде сперечатися, що результат спортсмена при стрибках у висоту залежить від фактора – «сила штовхаючої ноги». Так, цей фактор можна виміряти і в звичайних фізичних одиницях (ньютонах або побутових кілограмах), але коли?! Не під час же стрибка на змаганнях! Однак саме в цей робочий час фіксуються статистичні дані, накопичується матеріал для вихідної матриці.
Трохи складніше пояснити сутність самих процедур факторного аналізу простими елементарними поняттями (на думку деяких фахівців з області факторного аналізу – узагалі неможливо). Тому намагатимемося розібратися в цьому, використовуючи досить складний, але, на щастя, доведений у практичному змісті до повної досконалості, апарат векторної або матричної алгебри.
До того як стане зрозуміло необхідність у такому апараті, розглянемо основну теорему факторного аналізу. Суть її полягає в представленні моделі факторного аналізу (4.6) у матричному виді:
X[k×1] = B[k×m] × F[m×1] + Δ[k×1],(4.7)
і на наступному доведенні істинності виразу
R[k×k] = B[k×m] × B*[m×k],(4.8)
для «ідеального» випадку, коли нев’язки Δ дуже малі.
Тут B* [m×k] це транспонована матриця B [k×m].
Труднощі задачі пошуку матриці навантажень на фактори очевидна. Ще у шкільній алгебрі вказується на незліченну множину рішень системи рівнянь, якщо число рівнянь більше числа невідомих. Приблизний підрахунок говорить нам, що нам потрібно буде знайти km невідомих елементів матриці навантажень, у той час як тільки близько k2/2 відомих коефіцієнтів кореляції. Дещо допомагає доведене у теорії факторного аналізу співвідношення між даним коефіцієнтом парної кореляції (наприклад R12) і набором відповідних навантажень факторів: R12 = B11×B21 + B12×B22 + …+ B1m×B2m.
Таким чином, немає нічого дивного у твердженні, що факторний аналіз (а, виходить, і системний аналіз у сучасних умовах) – більше мистецтво, ніж наука. Тут важливо володіти «навичками» і надзвичайно важливо розуміти як потужність, так і обмежені можливості цього методу.
Є ще одна обставина, яка призводить до труднощів при професійній підготовці в області факторного аналізу. Це необхідність бути професіоналом у «технологічному» плані. Однак, з іншого боку, стати професіоналом високого рівня навряд чи можливо, не маючи хоча б уявлень про можливості аналізу й ефективно керувати системами на базі рішень, що знайдені за допомогою факторного аналізу.
Слід відзначити, що не треба зваблюватися вульгарними обіцянками популяризаторів факторного аналізу, не слід вірити міфам про його всемогутність й універсальність. Цей метод «на вершині» тільки за одним показником – своєю складністю, як по сутності, так і по складності практичної реалізації навіть при «повальному» використанні комп’ютерних програм. Прикладом є твердження про переваги методу головних компонентів – ніби, цей метод точніше розрахунку навантажень на фактори.
З цього приводу є один вислів відомого італійського статистика Карло Джинні. Він у вільному переказі звучить приблизно так: «Мені треба їхати в Мілан, і я куплю квиток на міланский потяг, хоча потяги на Неаполь ходять точніше і це підтверджено надійними статистичними даними. Чому? Так тому, що мені треба в Мілан…»...