6. ФУНКЦІЇ ТА НАЙПРОСТІШІ ГРАФІКИ
6.1. Область визначення і множина значень функції
Залежність змінної y від змінної х називається функцією, якщо кожному значення х відповідає єдине значення y. Змінну х називають незалежною змінною або аргументом, а змінну y – залежною змінною. Значення y, що відповідає заданому значенню х, називають значенням функції.
Записують: ![]() . Буквою
. Буквою ![]() позначається дана функція, тобто функціональна залежність між змінними х і y;
позначається дана функція, тобто функціональна залежність між змінними х і y; ![]() є значенням функції, що відповідає значенню аргументу х.
є значенням функції, що відповідає значенню аргументу х.
Всі значення, що їх набуває незалежна змінна, утворюють область визначення функції, її позначають ![]() або
або ![]() .
.
Всі значення, що їх набуває функція ![]() , утворюють область значень функції, яку позначають
, утворюють область значень функції, яку позначають ![]() або
або ![]() .
.
Функція в системі Maple визначається за допомогою оператора присвоювання (запам’ятовування) <:=>. Найпростіший спосіб задання функції f:=<аналітичний вираз>, наприклад від змінної х. Він незручний тим, що при такому заданні Maple ігнорує запис f(a) і значення f(a) потрібно обчислювати вбудованою функцією subs(x=a,f) – підставити ![]() в f:
в f:
> restart;
> f:=x^3;
![]()
> subs(x=4,f);
![]()
Існує спосіб задання функції в Maple за допомогою «стрілки», який не має того недоліку, що попередній спосіб. Він задається в такий спосіб: ![]() <вираз від х>, де стрілка вводиться як тире і знак більше. Наприклад,
<вираз від х>, де стрілка вводиться як тире і знак більше. Наприклад,
> f:=x->x^3;
![]()
> f(4);
![]()
Коли потрібно ввести функцію, яка задана декількома аналітичними виразами, можна використати оператор умовного переходу if, який застосовується в таких випадках:
1) if <умова> then <наслідок> fi;
Якщо виконується умова, то виконується наслідок. В іншому випадку нічого не виконується.
2) if <умова> then <наслідок 1> else < наслідок 2> fi;
Якщо виконано умову, то виконується наслідок 1, в іншому випадку виконується наслідок 2, що задається також компактним виглядом:
3) if (<умова>, <наслідок 1>, < наслідок 2>).
Нехай потрібно задати функцію 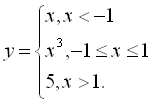
Конструкція 3, застосована двічі, дозволяє задати її в такому вигляді:
> restart;
> f:=`if`(x<-1,x,`if`(x<=1,x^3,5));
![]()
Обчислимо значення функції при ![]() :
:
> subs(x=-3,f);
![]()
> evalf(%);
![]()
Цей принцип використовується у вбудованій функції piecewise. За її допомогою дана функція вводиться так:
> f:=piecewise(х<-1,х,х<=1,х^3,x>1,5);

Приклад 1. Знайти область визначення і множину значень функцій:
а) ![]() ; б)
; б) 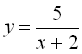 .
.
Розв’язання
а) ![]() . Оскільки область зміни х не вказано, природно областю визначення функції вважати множину всіх значень змінної х, при яких ця відповідність має сенс. Отже, у даному випадку
. Оскільки область зміни х не вказано, природно областю визначення функції вважати множину всіх значень змінної х, при яких ця відповідність має сенс. Отже, у даному випадку ![]()
![]() .
.
Легко збагнути, що ![]()
![]() . Знайдемо значення функції при декількох значеннях аргументу:
. Знайдемо значення функції при декількох значеннях аргументу: ![]() ,
, ![]() ,
,
![]() .
.
б) 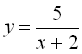 . Тут
. Тут ![]()
![]()
![]() . Для знаходження області значень
. Для знаходження області значень ![]() виразимо х через
виразимо х через ![]() :
: 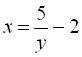 . Звідси видно, що
. Звідси видно, що ![]()
![]()
![]() . Знайдемо значення функції при деяких значеннях х:
. Знайдемо значення функції при деяких значеннях х:  ;
;  ;
; 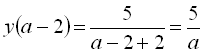 .
.
Приклад 2. Знайти область визначення функції  .
.
Розв’язання
Для того, щоб знайти область визначення функції  , розв’яжемо нерівність
, розв’яжемо нерівність 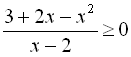
![]()

![]()
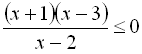 ;
;
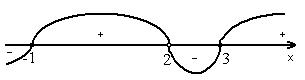
Тоді ![]()
![]()
![]() .
.
Відповідь: ![]()
![]()
![]() .
.


