7.3. Системи ірраціональних рівнянь

Приклад 12. Розв’язати систему рівнянь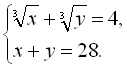

Розв’язання

ОДЗ: .

Розв’яжемо дану систему способом підстановки, для цього із другого рівняння системи виразимо через і підставимо у перше рівняння системи: 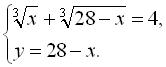. Окремо перетворимо перше рівняння системи, для цього піднесемо обидві його частини до кубу:

. Вираз замінимо на 4 (це випливає із властивості рівностей), тобто . Піднесемо обидві частини останнього рівняння до кубу і отримаємо .

Розв'язавши останнє квадратне рівняння, отримаємо корені тоді .

Відповідь: .

Приклад 13. Розв’язати систему рівнянь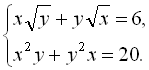

Розв’язання

ОДЗ: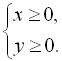

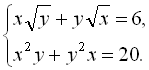
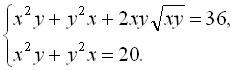
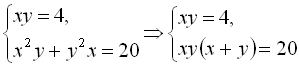Піднесемо до квадрата обидві частини рівняння (І) системи: Віднімемо від рівняння (І) рівняння (ІІ) системи і отримаємо , або Тоді або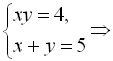

Відповідь:

> solve({x*sqrt(y)+y*sqrt(x)=6,x^2*y+y^2*x=20},{x,y});

     7.4. Ірраціональні нерівності   

При розв’язуванні ірраціональних нерівностей використовуються ті ж прийоми, що і при розв’язуванні ірраціональних рівнянь: зведення обох частин нерівності до того самого натурального степеня, введення нових змінних, відокремлення радикала і т. д.

Розглянемо найпростіші ірраціональні нерівності.

Приклад 14. Розв’язати нерівність .

Розв’язання

Область допустимих значень лівої частини нерівності , тобто 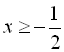. Звідси дістаємо, що початкова нерівність еквівалентна такій системі нерівностей:

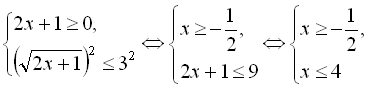Тобто

.

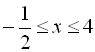Відповідь: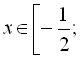

Для розв’язування ірраціональних нерівностей та систем нерівностей, як і раціональних нерівностей та їх систем, використовуємо команду solve(). Відповідь виражається або у вигляді множини нерівностей, або через функцію RealRaange() і Open(). Перша визначає замкнений відрізок дійсних чисел, а друга використовується, щоб вказати, що гранична точка не входить в побудований розв’язок. Для того, щоб задати розв’язок у вигляді множини, потрібно задати у вигляді множини або саму нерівність, або невідому, відносно якої вона розв’язується. Якщо цього не зробити, то відповідь буде отримана з використанням вказаних функцій визначення дійсних відрізків. Розглянемо це на попередньому прикладі:

> solve(sqrt(2*x+1)<=3,x);

> solve(sqrt(2*x+1)<=3,{x});

Приклад 15. Розв’язати нерівність

Розв’язання

Оскільки , то початкова нерівність виконується для всіх х з області визначення функції .

.

Відповідь:

> solve(sqrt(x-5)>=-3,{x});

Приклад 16. Розв’язати нерівність .

Розв’язання

Оскільки , то початкова нерівність не виконується при жодних значеннях х.

Відповідь: .

Розглянемо більш складні нерівності.

Ірраціональні нерівності виду розписують у вигляді системи нерівностей: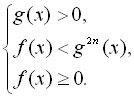

Ірраціональні нерівності виду розписують у вигляді

сукупності двох систем раціональних нерівностей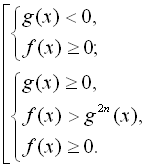

Іншими словами, розглядаються випадки, коли права частина нерівності від’ємна, і коли вона невід’ємна.

Приклад 17. Розв’язати нерівність .

Розв’язання

Якщо , то або, якщо , то і .

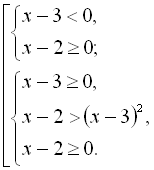
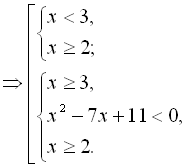
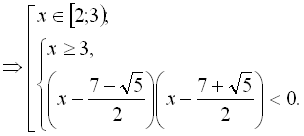
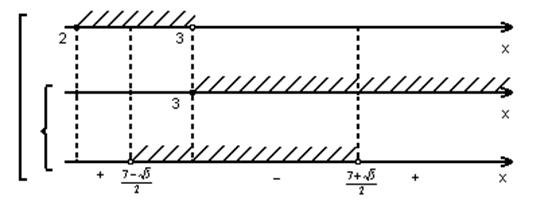
Відповідь:

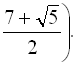
     Приклад 18. Розв’язати нерівність .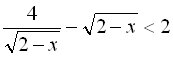

     Розв’язання

     Позначимо 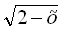через 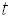, 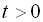. Тоді одержимо рівняння: , .

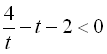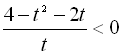Оскільки , то або Розкладемо на множники ліву частину отриманої нерівності:

; тобто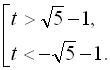

Повернувшись до заміни, маємо: 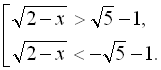Оскільки друга нерівність сукупності не має сенсу, то розв’яжемо першу нерівність сукуп-

ності.

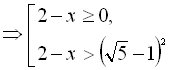
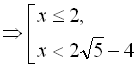
Відповідь:

> solve(4/sqrt(2-x)-sqrt(2-x)<2,{x});

Приклад 19. Розв’язати нерівність .

Розв’язання

Перенесемо один з радикалів в праву частину для того, щоб полегшити перетворення: .

Піднесемо обидві частини нерівності до квадрата і отримаємо:

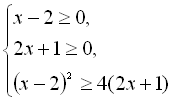
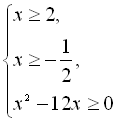
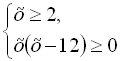
Відповідь:

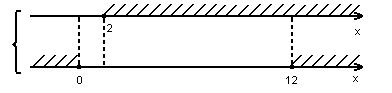
Приклад 20. Знайти цілі числа, які є розв’язками нерівності

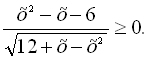
     Розв’язання

     Оскільки знаменник дробу, що стоїть у лівій частині нерівності, завжди додатний, то чисельник цього ж дробу буде невід’ємний. Тому дану нерівність розпишемо системою двох нерівностей:

.

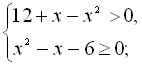
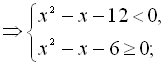
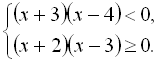
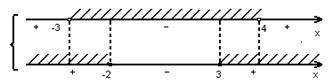
Правильність розв’язку перевіримо у системі Maple за допомогою функції solve:

> solve((x^2-x-6)/sqrt(12+x-x^2)>=0,{x});

;

а цілі значення, які входять у розв’язок, знайдемо за допомогою функції isolve:

> isolve((x^2-x-6)/sqrt(12+x-x^2)>=0,{x});

.

Відповідь: .