7.2. Метод введення нових змінних

Приклад 9. Розв’язати рівняння .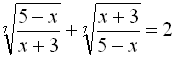

Розв’язання

Зробимо заміну змінної, поклавши 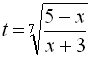. Тоді 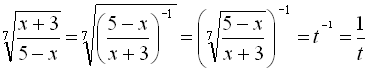. Звідси дістаємо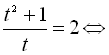 Оскільки робилися лише еквівалентні перетворення, то початкове рівняння рівносильне такому: .

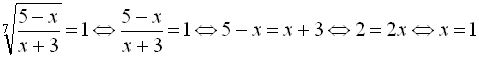При перевірці переконуємось, що – корінь вихідного рівняння.

Відповідь: .

Оскільки попереднє рівняння досить громістке і потрібно перевірити правильність його задання в системі Maple, то для розв’язання даного рівняння використовуємо smart-спосіб:

> ((5-x)/(x+3))^(1/7)+((x+3)/(5-x))^(1/7)=2;

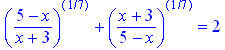
> {x = 1};

Приклад 10. Знайти добуток коренів рівняння

Розв’язання

Перетворимо дане рівняння

. Зробимо заміну , причому .

Звідси, . Тоді отримаємо:

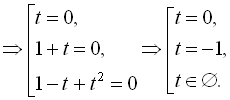
Отже , але умову задовольняє лише .

Повернемось до нашої заміни:

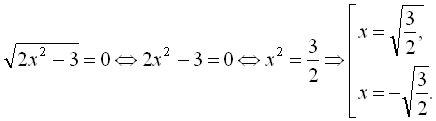
Отже, коренями вихідного рівняння є і 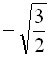, а їх добутком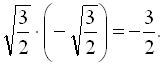

Відповідь:

Приклад 11. Розв’язати рівняння

.

Розв’язання

Зробимо заміну через , тоді .

Запишемо дане рівняння з новою змінною:

Останнє рівняння розв’язуємо методом інтервалів.

. Маємо три інтервали:

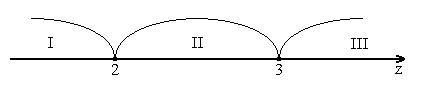
І:

ІІ:

ІІІ:

Для І інтервалу . Оскільки 2 входить в проміжок , то є розв’язком рівняння .

У ІІ інтервалі . Маємо правильну рівність, тобто весь інтервал є розв’язком рівняння .

Для ІІІ інтервалу маємо . Однак значення .

Враховуючи, що і , маємо , або .

Оскільки , то .

Остання подвійна нерівність є розв’язком рівняння .

Відповідь:

Спробуємо знайти розв’язок даного рівняння за допомогою Maple:

> eq:=sqrt(x+3-4*sqrt(x-1))+sqrt(x+8-6*sqrt(x-1))=1;

solve(eq,x);

Як бачимо, надзвичайно потужна команда solve виявилась безсильною. В подібних випадках потрібно застосовувати так звану технологію «штовхай та їдь». Суть технології полягає в тому, щоб допомогти системі подолати деякі складні для неї ланки на шляху розв’язання задачі, а далі система знову допомагатиме нам самим. Продемонструємо технологію на прикладі. Зробимо заміну:

> eq1:=subs(x=z^2+1,eq);

Наступним кроком повинне бути спрощення отриманого виразу. І тут потрібно бути уважним. Застосування команди спрощення виразу simplify без додаткових опцій приводить до надто складного рівняння

> eq2:=simplify(eq1);

розв’язок якого система знайти не в змозі:

> solve(eq2,z);

Застосування команди спрощення виразу simplify з опцією symbolic приво-

дить до отримання неправильного результату, оскільки в такому випадку

система перетворює корені за правилом замість :

> eq3:=simplify(eq1,'symbolic');

Правильним застосуванням команди simplify в даному випадку є таке:

> eq4:=simplify(eq1,assume=positive);

Зведемо подібні

> eq5:=collect(lhs(eq4),[signum(-2+z),signum(-3+z)])= rhs(eq4);

У цьому випадку ми отримали правильну відповідь, на жаль, у формі, що відрізняється від традиційної

> abs(z-2)+abs(z-3)=1;

Далі ми можемо піти двома шляхами: 1) спочатку розв’язати отримане рівняння відносно z, а потім знайти розв’язки для х; 2) спочатку підставити в рівняння замість z його значення через х, а потім розв’язати отримане рівняння через z. Підемо другим шляхом:

> subs(z=sqrt(x-1),eq5);

solve(%,x);

Відомо, в Maple RealRange(5,10) означає замкнений інтервал.

Як бачимо, в даному випадку команда solve виконала поставлене завдання.

> fsolve(h,x);

> subs(x=10,h);