7. ІРРАЦІОНАЛЬНІ РІВНЯННЯ ТА НЕРІВНОСТІ
7.1. Основні методи розв’язування ірраціональних рівнянь
Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.
В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння ![]() не має коренів, бо арифметичний корінь не може бути від’ємним.
не має коренів, бо арифметичний корінь не може бути від’ємним.
Рівняння ![]() не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази
не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази ![]() і
і ![]() нулю дорівнювати не можуть.
нулю дорівнювати не можуть.
Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.
При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння ![]() до парного степеня дістаємо рівняння, що є результатом не тільки рівняння
до парного степеня дістаємо рівняння, що є результатом не тільки рівняння ![]() , але і рівняння
, але і рівняння ![]() , оскільки і
, оскільки і ![]() , і
, і ![]() . Так, наприклад, візьмемо рівняння
. Так, наприклад, візьмемо рівняння ![]() . Піднісши обидві частини цього рівняння до квад-рата, дістанемо
. Піднісши обидві частини цього рівняння до квад-рата, дістанемо ![]()
![]()
![]() Коренями цього рівняння є числа
Коренями цього рівняння є числа ![]()
![]() Однак після перевірки переконуємось, що
Однак після перевірки переконуємось, що ![]() є коренем рівняння
є коренем рівняння ![]() , а
, а ![]() є побічним коренем.
є побічним коренем.
Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.
Розглянемо рівняння виду ![]() . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду
. Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду ![]() рівносильне такій системі:
рівносильне такій системі:
![]()
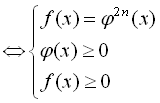 .
.
У системі Maple ірраціональні рівняння, як і раціональні, розв’язу-ються за допомогою функції solve(). Для позначення кореня використовуємо функцію sqrt ().
Приклад 1. Розв’язати рівняння ![]() .
.
Розв’язання
Дане рівняння можна звести до вигляду ![]() , тобто
, тобто ![]()
![]()
![]()
![]()
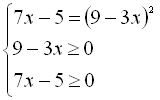
![]()
![]()
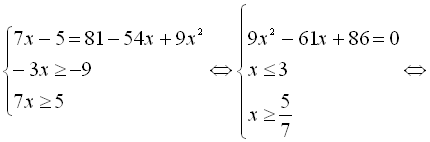
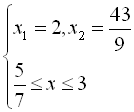 .
.
З даної системи випливає, що лише ![]() є коренем початкового рівняння.
є коренем початкового рівняння.
Відповідь: ![]() .
.
> solve({3*x+sqrt(7*x-5)=9},{x});
![]()
Розв’язання рівняння виду ![]() , де
, де ![]() , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
, здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.
Приклад 2. Розв’язати рівняння ![]() .
.
Розв’язання
Область визначення даного рівняння визначається в результаті розв’-
язання системи нерівностей 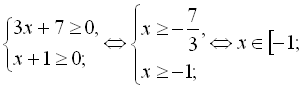
![]() .
.
Перетворимо дане рівняння:
![]()
![]()
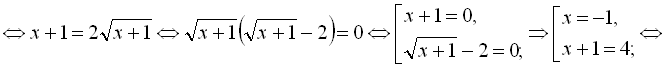
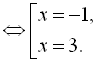
Обидва знайдені корені належать ОДЗ.
Відповідь: ![]()
![]() .
.
Приклад 3. Розв’язати рівняння ![]() .
.
Розв’язання
Знайдемо для початку область допустимих значень: 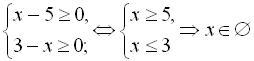 .
.
Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.
Відповідь: ![]() .
.
Таким чином, в даному прикладі попереднє знаходження ОДЗ виявилось надзвичайно корисним.
> solve(sqrt(x-5)+sqrt(3-x)=7);
![]()
Далі ми покажемо, як давати вказівку системі шукати корені тільки у множині дійсних чисел. За замовчуванням система шукає корені в комплексній області, тому система і видала комплексні корені.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв’язання
Обидва підкореневі вирази є повними квадратами, тому
![]()
![]()
Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.
Приклад розв’язання рівняння такого типу наводився раніше.
Відповідь: ![]()
![]() .
.
Рівняння виду ![]() можна розписати за допомогою змішаних систем:
можна розписати за допомогою змішаних систем:
![]()
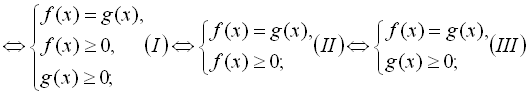
З наведених вище трьох систем вибирають звичайно ту, де простіше розв’язати нерівність (![]() або
або ![]() ). Якщо ж обидві нерівності
). Якщо ж обидві нерівності ![]() і
і ![]() розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
розв’язати нескладно, то можна вибрати першу систему, яка хоча і містить одну зайву нерівність, є більш наочною, ніж ІІ і ІІІ.
Приклад 5. Розв’язати рівняння ![]() .
.
Розв’язання
Для розв’язання даного рівняння обираємо ІІІ систему:
![]()
![]()
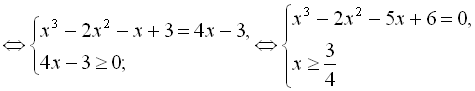 .
.
Окремо розв’яжемо рівняння ![]() нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді
нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: ±1; ±2; ±3. При підборі знаходимо, що коренями є -2; 1; 3. Тоді 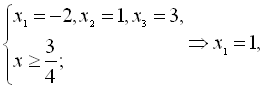
![]()
Відповідь: ![]()
![]()
Покажемо інший спосіб запису ірраціональних рівнянь у системі Maple, при якому корінь записуємо у вигляді степеня:
> solve((x^3-2*x^2-x+3)^(1/2)=(4*x-3)^(1/2));
![]()
> restart;
> assume(4*x-3>=0);
> solve(sqrt(x^3-2*x^2-x+3)=sqrt(4*x-3));
![]()
> restart;eval(sqrt(x^3-2*x^2-x+3)=sqrt(4*x-3),x=-2);
![]()
Приклад 6. Розв’язати рівняння ![]() .
.
Розв’язання
Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: ![]() , звідки
, звідки ![]() .
.
Перевірка: Підставивши ![]() в початкове рівняння, дістанемо
в початкове рівняння, дістанемо ![]() , тобто
, тобто ![]() – правильна рівність
– правильна рівність ![]() є коренем.
є коренем.
Відповідь: ![]() .
.
Приклад 7. Розв’язати рівняння ![]() .
.
Розв’язання
ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:
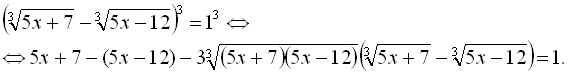
Замінимо різницю ![]() правою частиною первинного рівняння, тобто 1:
правою частиною первинного рівняння, тобто 1: ![]() .
.
Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу: ![]()
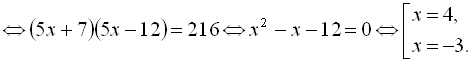
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є ![]()
![]() .
.
Відповідь: ![]()
![]() .
.
Ще простіше у системі Maple розв’язуються рівняння smart-способом – через контекстне меню:
1) в командний рядок вводиться рівняння і знаходиться його стандартний математичний вигляд (як при перевірці правильності введення);
2) клацанням ПКМ по виділеному стандартному математичному вигляду відкривається контекстне меню;
3) після клацання ЛКМ на рядок Solve (або, якщо змінних декілька, на потрібну змінну рядка Solve Equation for a Variable) у командному рядку наступної секції з’являються корені.
Покажемо розв’язання ірраціонального рівняння smart-способом на прикладі 7:
> (5*x+7)^(1/3)-(5*x-12)^(1/3)=1;
![]()
> {x = 4};
Як бачимо, при знаходженні коренів рівняння система один дійсний корінь ![]() «загубила». Більш того, навіть підстановка «загубленого» значення в рівняння не перетворює його на тотожність (!).
«загубила». Більш того, навіть підстановка «загубленого» значення в рівняння не перетворює його на тотожність (!).
> subs(x=-3,(5*x+7)^(1/3)-(5*x-12)^(1/3))=1;evalf(%);
![]()
![]()
На думку авторів [1] проблема полягає в тому, що «Maple испытывает затруднения при вычислениях уже целого ряда простых радикалов с рациональными степенями от отрицательных значений, если знаменатель экспоненты – нечетное число. В этом случае даже стандартная функция evalf оказывается бессильной» [1, С. 46]. Насправді ж уникнути подібних ситуацій можна за допомогою додаткового пакета RealDomain. Справа в тому, що система Maple, як уже зазначалось, за замовчуванням основною системою обчислень вважає область комплексних чисел. Підключення зазначеного пакета переключає основну систему на область дійсних чисел.
> with(RealDomain):
eq:=(5*x+7)^(1/3)-(5*x-12)^(1/3)=1;
solve(eq,x);
Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh
![]()
![]()
Як видно, після підключення пакета RealDomain вигляд раціонального виразу в лівій частині рівняння автоматично був змінений, що не завжди зручно. Але при цьому ми отримали всі корені рівняння (У версії Maple 7 все ж таки знаходиться тільки один корінь ![]() (!)). А підстановка будь-якого кореня рівняння перетворює його на тотожність:
(!)). А підстановка будь-якого кореня рівняння перетворює його на тотожність:
> eval(eq2,x=-3);simplify(%);
![]()
![]()
На жаль, і в цьому випадку зустрічаємось з деякими прикростями. Як видно, підстановка за допомогою команди eval (як і команди subs) не приводить до автоматичного здобуття наочної тотожності. Потрібно застосувати ще й команду спрощення simplify. В той же час наступна конструкція зразу приводить до отримання тотожності в бажаній формі:
> eval((5*x+7)^(1/3)-(5*x-12)^(1/3)=1,x=-3);
![]()
Особливості на цьому не закінчуються. Продовжимо цитату [1, С. 46]. «В этом случае даже стандартная функция evalf оказывается бессильной совместно с использованием пакетного модуля RealDomain, что очень хорошо иллюстрируют довольно простые примеры, а именно:
> restart:
R:=(58 + (-243)^(1/5) + (-8)^(2/3))*(10 + (-1331)^(2/3) + (-8)^(2/3))/((63 +(-32)^(4/5) - (-27)^
(2/3))* (17 + (343)^(2/3) + (-32)^(3/5)));
with(RealDomain):
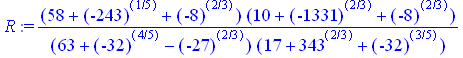
Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh
> evalf(R);
![]() »
»
Наведений приклад автори [1] використовують як обґрунтування необхідності доопрацювання стандартної команди evalf і пропонують власноруч розроблену команду Еvalf. Але наступна конструкція показує, що необхідність розробки процедури Еvalf насправді відсутня.
> restart:
with(RealDomain):
R:=(58 + (-243)^(1/5) + (-8)^(2/3))*(10 + (-1331)^(2/3) + (-8)^(2/3))/((63 +(-32)^(4/5) - (-27)^
(2/3))* (17 + (343)^(2/3) + (-32)^(3/5)));
evalf(R);
Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh
![]()
![]()
Потрібно, всього-на-всього, переставити місцями послідовність виконання команд системи, або ж після підключення пакета RealDomain повторно виконати команду присвоєння відповідного виразу.
Приклад 8. Розв’язати рівняння ![]() .
.
Розв’язання
Знайдемо ОДЗ даного рівняння:
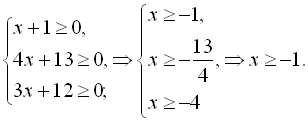
Піднесемо обидві частини рівняння до квадрата: ![]() . (1)
. (1)
Останнє рівняння мало б місце при ![]() тобто при
тобто при ![]() , але, враховуючи ОДЗ,
, але, враховуючи ОДЗ, ![]() , маємо, що
, маємо, що 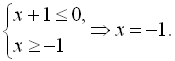
При перевірці дізнаємось, що ![]() є розв’язком рівняння (1). Оскільки рівняння (1) не має інших розв’язків, то і наше початкове рівняння має лише один розв’язок
є розв’язком рівняння (1). Оскільки рівняння (1) не має інших розв’язків, то і наше початкове рівняння має лише один розв’язок ![]() .
.
Відповідь: ![]() .
.


