8. ТРИГОНОМЕТРИЧНІ ПЕРЕТВОРЕННЯ
8.1. Радіанна система вимірювання кутів і дуг
Кут – це геометрична фігура, утворена двома променями, які виходять з однієї точки, названої вершиною кута (рис. 9). Слово “кут” заміняють символом Р: РАОВ=РВОА=Рa.
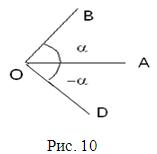
Кут можна розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки О. Промінь можна обертати навколо своєї початкової точки у двох напрямках: за годинниковою стрілкою і проти годинникової стрілки. Напрям обертання проти годинникової стрілки умовно називають додатним, а за годинниковою стрілкою – від’ємним. Відповідно до цього кути і дуги, отримані обертанням променя проти годинникової стрілки, вважаються додатними, а кути і дуги, отримані обертанням променя за годинниковою стрілкою, вважаються від’ємними (рис. 10).
Якщо сторони кута утворюють пряму, то такий кут називається розгорнутим. Якщо промінь робить повний оберт навколо своєї початкової точки, то отриманий кут називається повним.
Осі абсцис (Ох) і ординат (Оу) ділять повний кут (коло) на чотири чверті (I - IV), або чотири квадранта (рис. 11).
Кути вимірюються в градусах і радіанах. Кут в 1 градус – це кут, що його опише промінь, зробивши 1/360 частину повного оберту навколо своєї початкової точки проти годинникової стрілки (позначка 1?). 1/60 частина градуса називається хвилиною (позначка ![]() ). 1/60 частина хвилини називається секундою (позначка
). 1/60 частина хвилини називається секундою (позначка ![]() ).
).
Градусна міра в Maple degrees. Переведення радіанної міри кута (radians) в градусну і навпаки здійснюється вбудованою функцією convert.
Центральним кутом у колі називається кут, вершина якого знаходиться в його центрі.
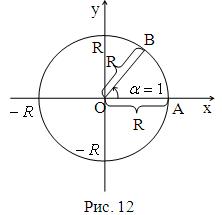
Кут в 1 радіан – це центральний кут, який спирається на таку дугу кола, довжина якої дорівнює радіусу цього кола. Слово “радіан” звичайно не пишуть. Таким чином, якщо |АВ|=R, |OA|=|OB|=R, то РАОВ=Рa=1, тобто кут a дорівнює одному радіану (рис. 12).
Оскільки довжина всього кола дорівнює 2?R, то повний кут складає ![]() радіан, тому що
радіан, тому що 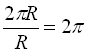 . Оскільки повний кут дорівнює 360°, то
. Оскільки повний кут дорівнює 360°, то ![]() 360°. Звідси 1 радіан =
360°. Звідси 1 радіан = 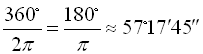 (57 градусів, 17 хвилин, 45 секунд).
(57 градусів, 17 хвилин, 45 секунд).
Таким чином, користуючись співвідношеннями ![]() ,
, 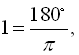
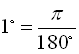 , можна переходити від градусів до радіанів і навпаки.
, можна переходити від градусів до радіанів і навпаки.
Приклад 1. а) Виразити в радіанах кут у 45°;
б) Виразити в градусах кут у 3 радіана.
Розв’язання
а) 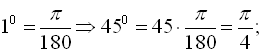
б) 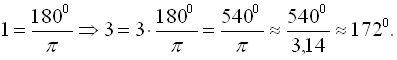
У системі Maple перехід від градусної міри кута до радіанної здійснюється майже так само, як і звичайним способом:
> 30*Pi/180;
![]()
> 45*Pi/180;
![]()
8.2. Визначення тригонометричних функцій
Розглянемо спочатку тригонометричні функції гострого кута, які можна ввести за допомогою прямокутного трикутника (рис. 13).
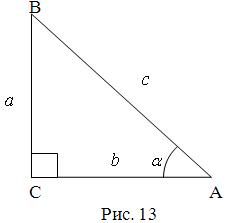
Нехай у прямокутному трикутнику ACB ![]()
![]() (відношення протилеж-ного катета до гіпотенузи).
(відношення протилеж-ного катета до гіпотенузи).
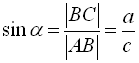 (відношення прилеглого катета до гіпотенузи).
(відношення прилеглого катета до гіпотенузи).
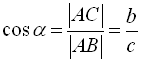 (відношення протилеж-ного катета до прилеглого).
(відношення протилеж-ного катета до прилеглого).
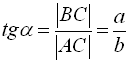 (відношення прилег-лого катета до протилежного).
(відношення прилег-лого катета до протилежного).
Розглянемо тригонометричні функції довільних значень аргументу.
Маємо прямокутну систему координат x0y на площині і коло одиничного радіуса, що має центр у початку координат (рис. 14). Таке коло називається одиничним колом чи тригонометричним колом. Відзначимо на осі 0х справа від початку координат точку 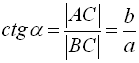 , яка лежить на тригонометричному колі:
, яка лежить на тригонометричному колі: ![]()
![]() . Радіус
. Радіус ![]() називається початковим радіусом. При повороті початкового радіуса
називається початковим радіусом. При повороті початкового радіуса ![]() навколо центра 0 на кут
навколо центра 0 на кут ![]() точка
точка ![]()
![]() переходить в деяку точку
переходить в деяку точку ![]()
![]() .
.
![]()
Синусом кута
називається відношення ординати точки ![]() до радіуса.
до радіуса.
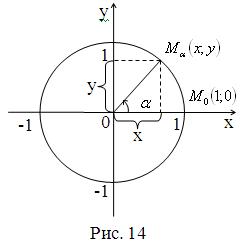
Косинусом кута ![]() називається відношення абсциси точки
називається відношення абсциси точки ![]() до радіуса.
до радіуса.
Таким чином, ![]() ,
, 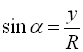 . Оскільки
. Оскільки 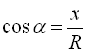 , то
, то ![]() ,
, ![]() .
. ![]() і
і ![]() можна розглядати як проекції на осі координат одиничного вектора
можна розглядати як проекції на осі координат одиничного вектора ![]() . Таким чином, можна стверджувати, що синус кута
. Таким чином, можна стверджувати, що синус кута ![]() дорівнює ординаті, а косинус – абсцисі вектора одиничної довжини, що виходить з початку координат і утворює з додатним напрямом осі
дорівнює ординаті, а косинус – абсцисі вектора одиничної довжини, що виходить з початку координат і утворює з додатним напрямом осі ![]() кут
кут ![]() . Оскільки координати будь-якої точки
. Оскільки координати будь-якої точки ![]()
![]() одиничного кола задовольняють рівняння
одиничного кола задовольняють рівняння ![]() , то
, то ![]() .
.
Співвідношення ![]() (1) називається основною тригонометричною тотожністю.
(1) називається основною тригонометричною тотожністю.
Тангенсом кута ![]() називається відношення ординати точки
називається відношення ординати точки ![]() до її абсциси:
до її абсциси: ![]() . (2)
. (2)
Котангенсом кута 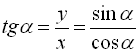 називається відношення абсциси точки
називається відношення абсциси точки ![]() до її ординати:
до її ординати: ![]() . (3)
. (3)
Секансом кута 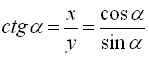 (позначення
(позначення ![]() ) називається величина, обер-нена
) називається величина, обер-нена ![]() , тобто
, тобто ![]() ,
, 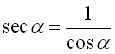 . (4)
. (4)
Косекансом кута ![]() (позначається
(позначається ![]() ) називається величина, обернена
) називається величина, обернена ![]() , тобто
, тобто ![]() ,
, 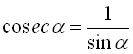 . (5)
. (5)
Позначення тригонометричних функцій в системі Maple:
sin, cos, tan, cot, sec, csc.
Обернені тригонометричні функції відповідно позначаються:
arcsin, arccos, arctan, arccot, arcsec, arccsc.
З повним списком математичних функцій, які входять у Maple, і їх позначеннями рекомендується ознайомитись самостійно. Наберіть inifen, виділіть і натисніть
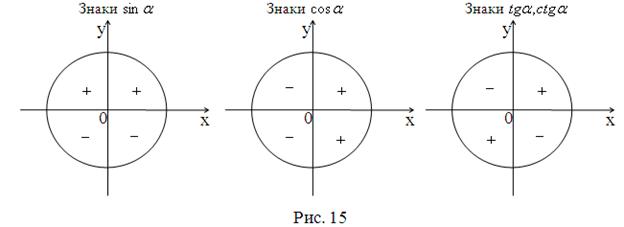
Знаки тригонометричних функцій наведені на рис. 15.
![]()
Зобразимо таблицю значень тригонометричних функцій деяких кутів, які найбільш часто використовуються на практиці (табл. 4).
Таблиця 4 – Значення тригонометричних функцій для деяких значень аргументу
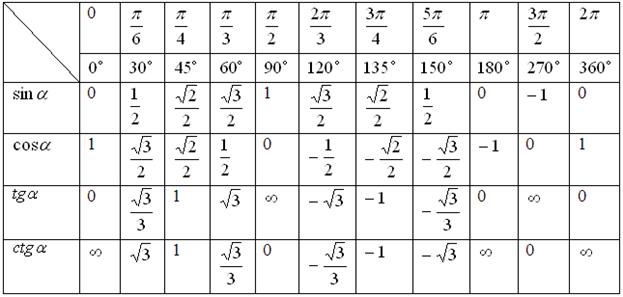
Символ (нескінченність) означає, що ![]() або
або ![]() при відповідних значеннях аргументу не визначені і набувають великих значень за модулем.
при відповідних значеннях аргументу не визначені і набувають великих значень за модулем.
Основні співвідношення між тригонометричними функціями того самого аргументу
З означення тангенса та котангенса кута, ми отримали тригонометричні тотожності ![]() і
і 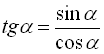 . Перемноживши їх між собою, отримаємо:
. Перемноживши їх між собою, отримаємо:
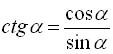 , тобто
, тобто 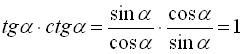 . (6)
. (6)
Розділивши почленно основну тригонометричну тотожність (1) на ![]() , отримаємо:
, отримаємо:
![]()
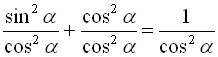
![]() (7)
(7)
Розділимо почленно 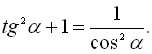 на
на ![]() і отримаємо
і отримаємо ![]() . (8)
. (8)


