8.3. Вираз одних тригонометричних функцій через інші

З основної тригонометричної тотожності випливає, що , тоді

,                    (9)

а отже .                                        (10)

У формулах (9) і (10) знаки «+» або «–» вибираються в залежності від того, у якій чверті закінчується кут . Так, якщо закінчується в І або ІІ чверті, то беремо знак «+», якщо в ІІІ або ІV чверті, то знак «–» у формулі (9). У формулі (10) для кутів, що закінчуються в І або ІV чвертях, потрібно взяти знак «+», а якщо кути закінчуються в ІІ або ІІІ чвертях, то знак «–».

Виразимо через з формули (8):

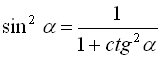
.                    (11)

З формули (6) випливає, що 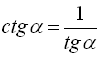, тоді формулу (11) можна записати через :

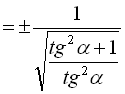
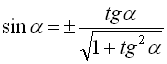.          (12)

З формули (7) слідує, що 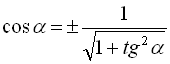,                    (13)

або через буде мати вигляд .          (14)

Приклад 2. Визначити знаки виразів: а) ; б) .

Розв’язання

Зазначимо, що , але, з іншого боку, радіан. Тому 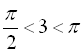, 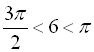. Звідси кут закінчується в ІІ чверті, а кут закінчується в ІV чверті. Тоді за таблицею знаків тригонометричних функцій, , .

Відповідь: а) ; б) .

Якщо задати в Maple обчислити, наприклад, , то одержимо результат в десяткових дробах:

> evalf(cos(6));

З отриманого результату видно, що знак виразу додатний.

Приклад 3. Обчислити .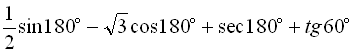

Розв’язання

За таблицею значень тригонометричних функцій, знаходимо:

.

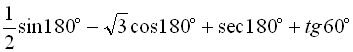
Відповідь: .

Приклад 4. Обчислити значення усіх тригонометричних функцій кута , якщо ,.

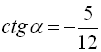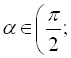
Розв’язання

Застосовуючи формули (8), (12), (10), (6), (4), (5), маємо 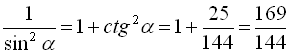, звідки 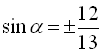, а оскільки у другій чверті синус додатний, то знаходимо 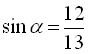. Далі 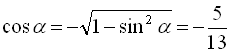(оскільки косинус від’ємний у другій чверті), , , .

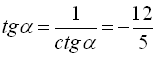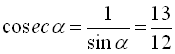Відповідь: ; ; ; ; .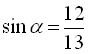

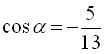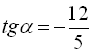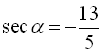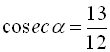Приклад 5. Спростити вираз .

Розв’язання

Розкладемо суму кубів і, застосовуючи формулу (1), дістаємо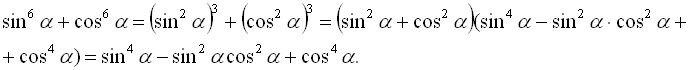

Далі маємо

.

Відповідь: .

Приклад 6. Спростити вираз 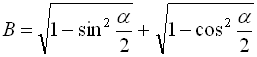, якщо

.

Розв’язання

З основної тригонометричної тотожності випливає, що .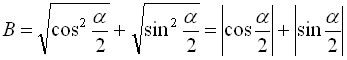

Оскільки , то 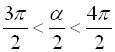, отже кут закінчується в ІV чверті, тоді 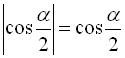, 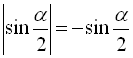. Звідси .

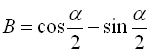Відповідь: .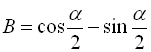

> restart:

simplify(sqrt(1-(sin(x/2))^2)+sqrt(1-(cos(x/2))^2));

> simplify(sqrt(1-(sin(x/2))^2)+sqrt(1-(cos(x/2))^2), assume=[x>3*Pi,x<4*Pi]);

На даному прикладі, розглянутому в Maple, можна прослідкувати відмінність спрощення тригонометричного виразу без накладання умов і з накладанням умов. Зазначимо, що команда assume задана дещо в іншому вигляді, як ми раніше її задавали. Ця структура assume задається у поєднанні з командою simplify.

Також звернемо увагу на те, що результат 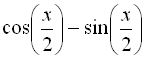ми отримали у версії Maple 9.5, у версії Maple 7 так не виходить, але це частковий прояв загальновідомої проблеми Maple – відсутність сумісності. «Отсутствует совместимость релизов пакета Maple «снизу-вверх»».

Приклад 7. Дано: . Знайти: а) ;

б) .

Розв’язання

а) Піднесемо обидві частини початкового виразу до квадрата:

;

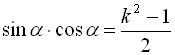б)

.

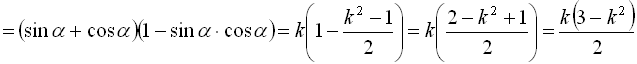В даному прикладі ми врахували, що якщо , то 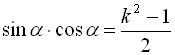відповідно до висновку пункту а).

Відповідь: а) 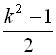; б) 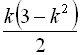.