8.4. Формули додавання і віднімання аргументів

Для будь-яких дійсних чисел і справедливі формули:

;                              (15)

;                              (16)

;                              (17)

;                              (18)

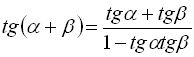;                                        (19)

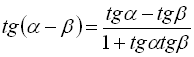.                                        (20)

Формула (19) справедлива при відмінних від 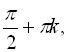. Формула (20) справедлива при відмінних від .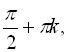

Приклад 8. Обчислити .

Розв’язання

Для початку можна розписати, як . Скориставшись формулою (16), при , отримаємо . Користуючись таблицею значень тригонометричних функцій, маємо

.

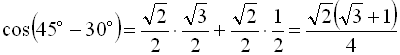Отже, .

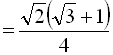Відповідь: .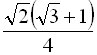

Приклад 9. Знайти 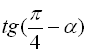, якщо .

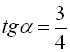Розв’язання

Скористаємося формулою (20) і врахуємо, що 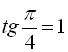. Маємо .

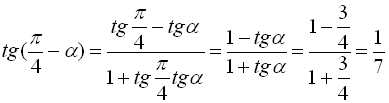Відповідь: .

Розглянемо приклад 9 в системі Maple двома способами:

> restart:

`1–й спосіб`;

tan(Pi/4-alpha);

expand(%);

eval(%,cot(alpha)=4/3);

Звернемо увагу на те, що коли ми задаємо вираз 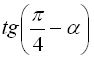, то він виводиться на екран як 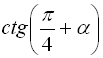, тобто система автоматично застосовує формули зведення. Потім, за допомогою команди expand(%), розкриваємо дужки. Вираз, отриманий в результаті, містить тригонометричну функцію , тому і значення потрібно підставляти для котангенса.

> `2-й спосіб`;

tan(beta-alpha);

expand(%);

eval(%,[tan(alpha)=3/4,beta=Pi/4]);

У другому способі ми замінили через , і система розкладає формулу , а потім за допомогою команди eval підставили значення 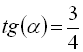і .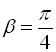

Якщо у першому способі ми підставляємо значення , а не , то система, звичайно, не видає потрібного результату:

> expand(tan(Pi/4-alpha));

> eval(%,tan(alpha)=3/4);

Як бачимо, звичний нам символ «» у Maple замінюється на «alpha», а символ «» – на «beta».