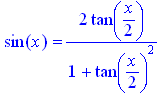8.5. Основні формули тригонометрії
Крім тригонометричних формул, з якими ми познайомилися раніше, існує ряд формул, що їх відносять до основних формул тригонометрії, а саме:
![]() ; (21)
; (21)
![]() ; (22)
; (22)
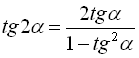
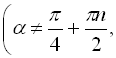
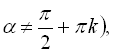
![]()
![]() ; (23)
; (23)
![]() ; (24)
; (24)
![]() ; (25)
; (25)
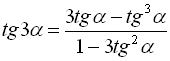 . (26)
. (26)
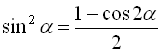 ; (27)
; (27)
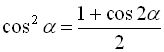 . (28)
. (28)
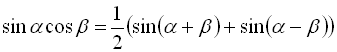 ; (29)
; (29)
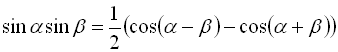 ; (30)
; (30)
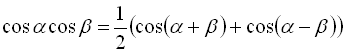 . (31)
. (31)
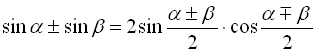 ; (32)
; (32)
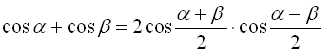 ; (33)
; (33)
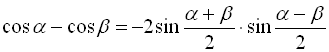 ; (34)
; (34)
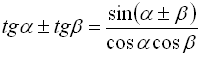
![]()
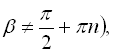
![]() ; (35)
; (35)
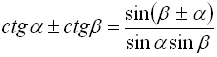
![]()
![]()
![]() . (36)
. (36)
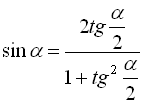 ; (37)
; (37)
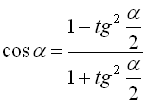
![]()
![]() ; (38)
; (38)
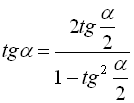
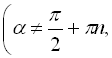
![]()
![]()
![]() . (39)
. (39)
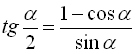
![]()
![]() ; (40)
; (40)
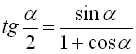
![]()
![]() ; (41)
; (41)
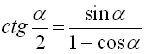
![]()
![]() ; (42)
; (42)
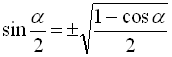 ; (43)
; (43)
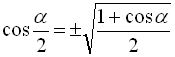 ; (44)
; (44)
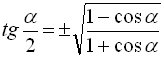 . (45)
. (45)
Знак перед радикалом в останніх трьох формулах залежить від того, в якій координатній чверті знаходиться кут ![]() .
.
В системі Maple, звичайно, закладені основні тригонометричні формули. Виводяться вони за допомогою вбудованих функцій для спрощення виразів, розкладання на множники, розкриття дужок і т.д., які описані в темі 1 даного практикуму.
> simplify(cos(x)^2+sin(x)^2);
![]()
> expand(sin(2*x));
![]()
> expand(cos(2*x));
![]()
> expand(tan(2*x));
![]()
> expand(cot(2*x));
![]()
> combine(cos(x)^2);
![]()
> combine(sin(x)^2);
![]()
> expand(sin(3*x));
![]()
> expand(cos(3*x));
![]()
> expand(cos(x+y));
![]()
> expand(sin(x+y));
![]()
> expand(tan(x+y));
![]()
> expand(cot(x+y));
![]()
> combine(sin(x)*cos(y));
![]()
> combine(cos(x)*cos(y));
![]()
> combine(sin(x)*sin(y));
![]()
Як бачимо, досить зручно використовувати Maple, якщо ви, наприклад, забули ту чи іншу тригонометричну формулу. Можливий випадок, коли вибрана користувачем команда не в змозі виконати ніяких перетворень, тоді система повертає вихідний тригонометричний вираз. Наприклад,
> simplify(tan(2*x));
![]()
Що стосується формул перетворення суми і різниці однойменних тригонометричних функцій у добуток, то О. Сдвижков [14] зазначає: «Удивительно, но ни одна из встроенных функций не преобразует сумму тригонометрических функций в произведение, какие бы дополнительные параметры ни устанавливались. В частности
> simplify(cos(x)+cos(у));
![]() »
»
Але це не відповідає дійсності, оскільки перетворення суми тригонометричних функцій в добуток можна здійснити за допомогою вбудованої функції trigsubs:
> trigsubs(cos(a*x)+cos(b*y));
trigsubs(cos(a*x)-cos(b*y));
trigsubs(-cos(a*x)+cos(b*y));
![]()
![]()
![]()
> trigsubs(sin(a*x)+sin(b*y));
trigsubs(sin(a*x)-sin(b*y));
trigsubs(-sin(a*x)+sin(b*y));
![]()
![]()
![]()
В той же час в наведених нижче простих випадках ця команда вже не спрацьовує
> trigsubs(-cos(a*x)-cos(b*y));
trigsubs(-sin(x)-sin(y));
Error, (in trigsubs) expecting a sum or difference of two functions but got -cos(a*x)-cos(b*y)
Error, (in trigsubs) expecting a sum or difference of two functions but got -sin(x)-sin(y)
Система Maple має тисячі команд. На жаль, авторам не відомо видання, в якому було б наведено систематичне ґрунтовне описання всіх команд цієї системи. В певній мірі саме з цим пов’язані подібні прикрі непорозуміння. Слід зауважити, що про існування команди trigsubs автори дізнались випадково на восьмому році «тісного» знайомства з цією системою. В жодному з джерел серед найпоширеніших публікацій з системи Maple [див. окремий файл «Список літератури з Maple.doc»] автори не знайшли посилання на команду trigsubs. Що ж стосується довідкової системи Maple, то при всіх її перевагах вона не усуває проблему відсутності зазначеного ґрунтовного описання всіх команд цієї системи. Звісно ж англомовність довідкової системи створює додаткові, хоча й не принципові, ускладнення. На щастя, Maple має власну вбудовану мову програмування, за допомогою якої можна відносно просто реалізувати широке коло потрібних перетворень. Як приклад, наведемо авторську процедуру, що перетворює суму (різницю) синусів або косинусів:
> scpm:=(f)->
if hasfun(f,{sin,cos}) then
L1:=[op(f)];L2:=map(zz->op(0,zz),L1);
if hasfun(f,cos) then
if L2[1]=cos and L2[2]=cos then
otv:=2*cos((op(1,L1[1])+op(1,L1[2]))/2)*cos((op(1,L1[1])-op(1,L1[2]))/2)
elif L2[1]=cos and op([2,2,0],L1)=cos then
otv:=-2*sin((op(1,L1[1])+op([2,2,1],L1))/2)*sin((op(1,L1[1])-op([2,2,1],L1))/2)
elif op([1,2,0],L1)=cos and L2[2]=cos then
otv:=-2*sin((op([1,2,1],L1)+op(1,L1[2]))/2)*sin((-op([1,2,1],L1)+op(1,L1[2]))/2)
else `Результат відсутній`;
fi;
elif hasfun(f,sin) then
if L2[1]=sin and L2[2]=sin then
otv:=2*sin((op(1,L1[1])+op(1,L1[2]))/2)*cos((op(1,L1[1])-op(1,L1[2]))/2)
elif L2[1]=sin and op([2,nops(L1[2]),0],L1)=sin then
otv:=2*cos((op(1,L1[1])+op([2,2,1],L1))/2)*sin((op(1,L1[1])-op([2,2,1],L1))/2)
elif op([1,nops(L1[1]),0],L1)=sin and L2[2]=sin then
otv:=2*cos((op([1,2,1],L1)+op(1,L1[2]))/2)*sin((-op([1,2,1],L1)+op(1,L1[2]))/2)
else `Результат відсутній`;
fi;
fi;
else `Результат відсутній`;
otv
fi;
Warning, `L1` is implicitly declared local to procedure `scpm`
Warning, `L2` is implicitly declared local to procedure `scpm`
Warning, `otv` is implicitly declared local to procedure `scpm`
> scpm(sin(a*x)+sin(b*y));
![]()
> scpm(cos(a*x)-cos(b*y));
![]()
> scpm(-sin(6*x)+sin(10*y));
![]()
> scpm(-cos(a*x)-cos(b*y));
![]()
Очевидно, що наведеною процедурою користуватися незрівнянно зручніше, аніж чотирма процедурами, що наведені в [14]. І справа не тільки в тому, що однією й тією ж самою процедурою користуватися легше, аніж чотирма процедурами. Головна перевага в тому, що процедури, які наведені в [14], потрібно вибирати в залежності від перетворюваного виразу. В процедурі scpm вираз, який потрібно перетворити, розпізнається автоматично! Якщо вираз, що переданий процедурі scpm як аргумент, не є сумою (різницею) синусів або косинусів, процедура повертає повідомлення «Результат відсутній». Важливо, що наведена процедура scpm працює і в DEMO Maple V R4 (!), в середовищі якої заблокована побудова процедур за допомогою стандартної конструкції proc…end proc.
В [14] також зауважується «Имеет смысл добавить также формулы, выражающие ![]() и
и ![]() через тангенс половинного аргумента:
через тангенс половинного аргумента:
> st:=proc(х)
2*tan(x/2)/(1+tan(x/2)^2)
end proc;
sin(x)=st(x);
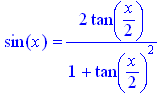 »
»
Насправді останню тотожність можна отримати стандартними засобами Maple, а саме за допомогою команди convert:
> sin(x)=convert(sin(x),tan);