8.6. Формули зведення

Формулами зведення називаються співвідношення, за допомогою яких значення тригонометричних функцій аргументів 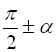, , , 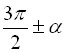виражаються через значення , , , .

Для полегшення запам’ятовування формул зведення можна користуватися такими правилами:

1) якщо у формулах містяться кути і , то найменування функції не змінюється; якщо ж у формулах містяться кути і , то найменування функції змінюється на подібне (синус – на косинус, тангенс – на котангенс і навпаки);

2) щоб визначити знак у правій частині формули («+» або « –»), досить, вважаючи кут гострим, визначити знак виразу, який стоїть у лівій частині формули; при цьому перед функцією кута ставлять такий знак, який має зведена функція кутів , , , .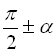

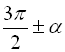Наприклад, ; .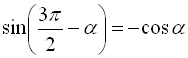

Приклад 10. Звести до тригонометричної функції гострого кута:

а) ; б) .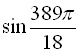

Розв’язання

Врахуємо, що період для і дорівнює або .

а);

б)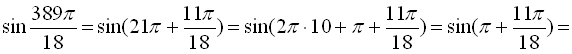

.

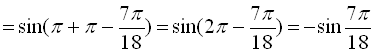Відповідь: а) ; б) .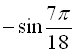

> evalf(cos(2009(degrees)));

> evalf(sin(389*Pi/18));

Знову одержали результат в десяткових дробах. Не важко перевірити, що він буде достовірним.

Приклад 11. Обчислити .

Розв’язання

Виконаємо перетворення, враховуючи періодичність:

;

;

;

.

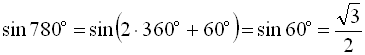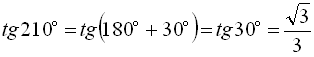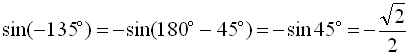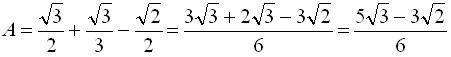Відповідь: .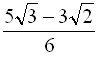

8.7. Приклади на доведення тригонометричних тотожностей

При доведенні тотожностей звичайно використовують такі способи:

1) Вираз, який стоїть в одній частині тотожності, за допомогою тотожних перетворень приводять до виразу, який стоїть в іншій частині тотожності;

2) вираз, який стоїть у лівій і правій частинах тотожності, приводять до одного і того ж виду;

3) доводять, що різниця між лівою і правою частинами тотожності дорівнює нулю.

Для доведення тригонометричних тотожностей в системі Maple вбудовано функцію testeq. На прикладах розглянемо, як дана функція застосовується.

Приклади 12 – 14. Довести тотожності:

12) .

Розв’язання

Перетворимо ліву частину даної тотожності:

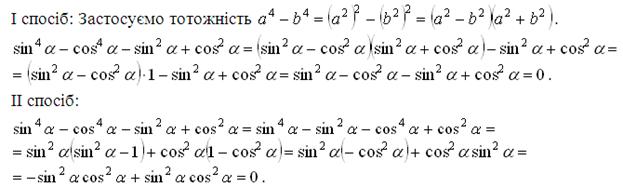
> (sin(alpha))^4-(cos(alpha))^4-(sin(alpha))^2+(cos(alpha)^2)=0;

> testeq((sin(alpha))^4-(cos(alpha))^4-(sin(alpha))^2+(cos(alpha)^2)=0);

У прикладі 12 ми спочатку ввели даний вираз, щоб переконатися, що ми це зробили правильно, а потім вже доводили дану тотожність. Варто звернути увагу, яким чином потрібно тригонометричну функцію підносити до степеня.

Система нам видала «true», тому дана тотожність справедлива.

13) .

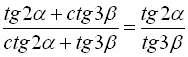Розв’язання

Позначимо ліву частину рівності А, а праву – В:

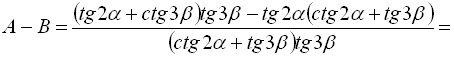
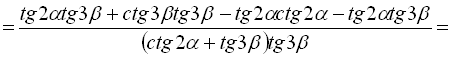
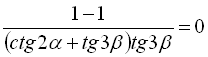, тобто . Тотожність доведено.

>testeq((tan(2*(x))+cot(3*(y)))/(cot(2*(x))+tan(3*(y)))=tan(2*(x))/tan(3*(y)));

14) .

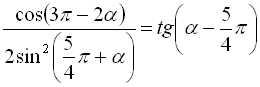Розв’язання

Спростимо ліву частину тотожності, яку потрібно довести:

.

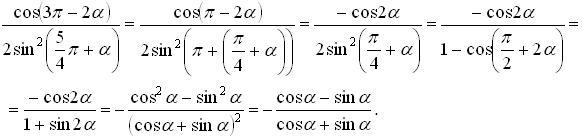Тепер спростимо праву частину даної тотожності:

.

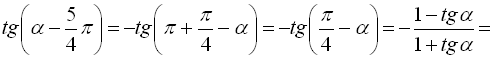
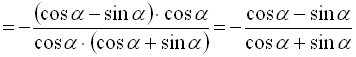Як бачимо, ліва і права частини однакові. Тотожність доведено.

8.8. Розв’язування прикладів на спрощення тригонометричних виразів

Приклад 15. Спростити вираз .

Розв’язання

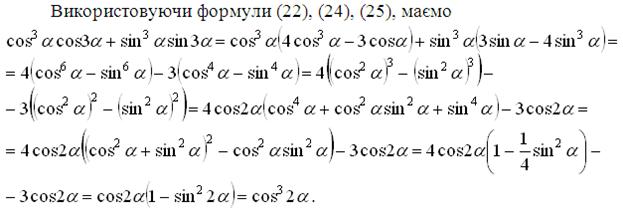Відповідь: .

Приклад 16. Спростити та обчислити

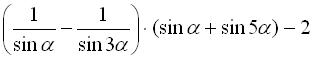, якщо .

Розв’язання

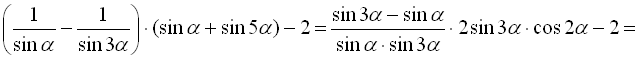
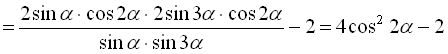. Якщо , тоді

.

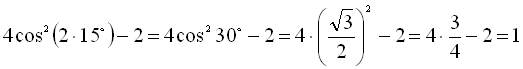Відповідь: 1.

>(1/sin(alpha)-1/sin(3*alpha))*(sin(alpha)+sin(5*alpha))-2;

> 16*cos(alpha)^4-16*cos(alpha)^2+2;

> p:=simplify((1/sin(alpha)-1/sin(3*alpha))*(sin(alpha)+sin(5*alpha))-2);

> o:=subs(alpha=15(degrees),p);

> evalf(o);

Приклад 17. Спростити та обчислити

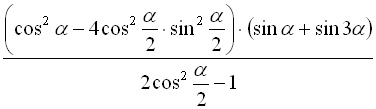, якщо .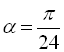

Розв’язання

.

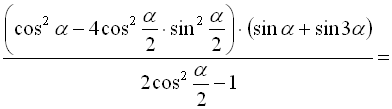
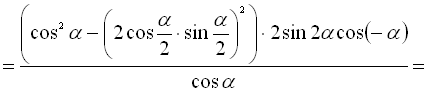
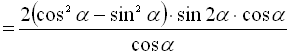
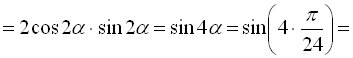
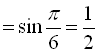Відповідь: .

Приклад 18. Перетворити у добуток вираз .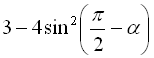

Розв’язання

.

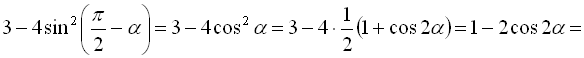
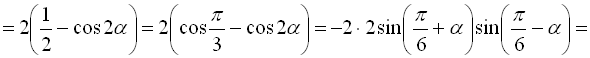
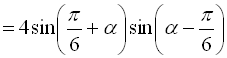Відповідь: .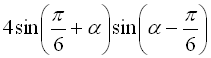

Якщо у системі Maple завданням буде перетворення виразу у добуток, то використовуємо функцію factor:

> factor(3-4*(sin(Pi/2-x))^2);

Як бачимо, система видала не той результат, що ми очікували, адже при спрощенні виразу аналітичним способом ми користувалися способом введення допоміжного кута, який Maple не розуміє.

Якщо скористаємось функцією combine, результат буде вже іншим:

> combine(3-4*(sin(Pi/2-x))^2);

.

Приклад 19. Обчислити

.

Розв’язання

За формулами зведення маємо ; ; ;…;

.

Тоді вираз можна записати в такий спосіб:

Відповідь: 1.